Предмет: Геометрия,
автор: kirill2449628
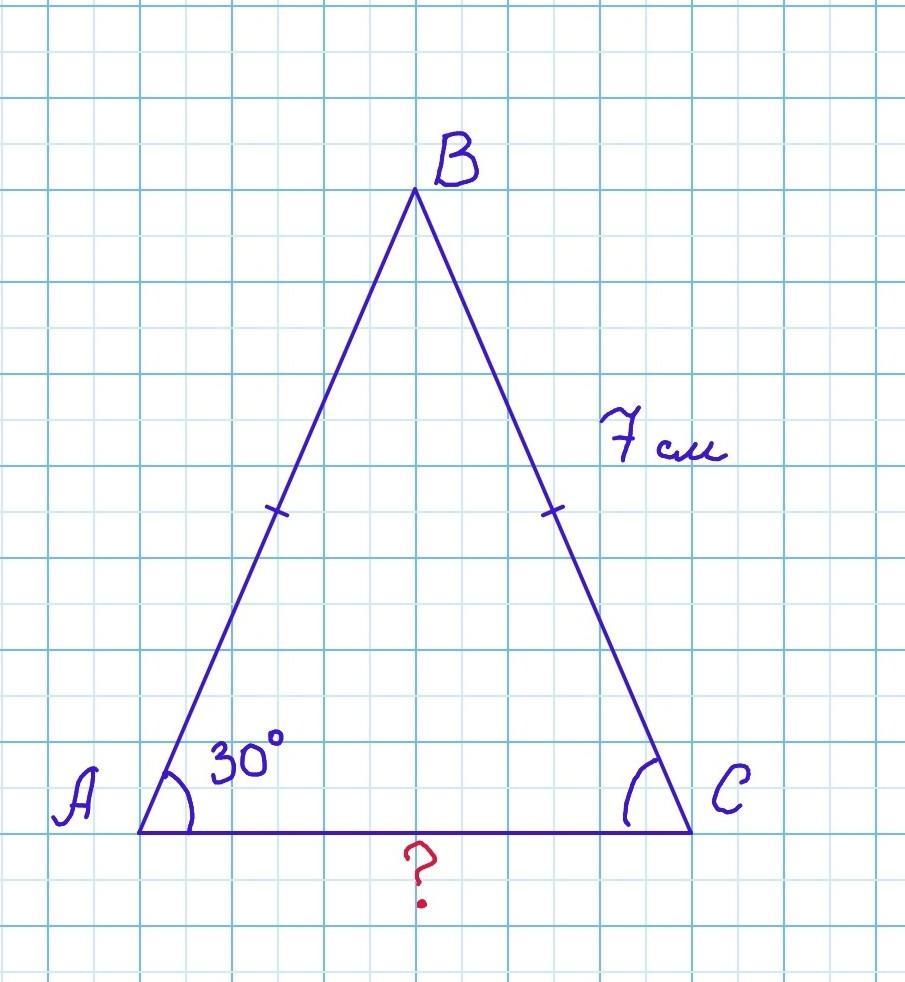
Длина боковой стороны равнобедренного треугольника ABC равна 7 см, а угол при основании равен 30°. Найди длину основания
Приложения:
goustricher:
7 под корнем 3
7 корней из трех. Я нашел угол B, а потом через него составил пропорцию. Получилось: 7 разделить на 1/2 = АС / Корень из 3 деленное на 2. И решаю эту пропорцию, получилось 7 корней из 3.
Правильный ответ:7√3
правильно
Ответы
Автор ответа:
1
Ответ:
7√3 см
Объяснение:
Так как треугольник равнобедренный, то его боковые стороны и углы при основании равны:
АВ = ВС = 7 см, ∠А = ∠С = 30°
По теореме синусов: Стороны треугольника пропорциональны синусам противолежащих углов,
имеем:
Основание АС = 7√3 см
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Алина00020003
Предмет: Алгебра,
автор: YouVokal
Предмет: Математика,
автор: dfasfd11
Предмет: Информатика,
автор: Nematullaevaybek
Предмет: Информатика,
автор: Nematullaevaybek