Предмет: Геометрия,
автор: Аноним
Параллельные прямые, их признаки и свойства. Урок 1
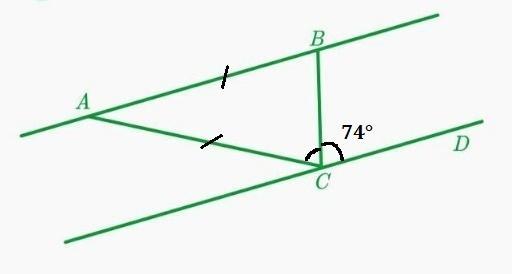
На рисунке AB = AC, CB — биссектриса угла ACD, ∠BCD = 74°.
Верных ответов: 3
AB ∥ CD
∠ABC = 74°
AB ∦ CD
∠ABC = 37°
ABC – разносторонний треугольник
ABC – равнобедренный
1.AB ∥ CD
2.ABC – равнобедренный
3.∠ABC = 74°
2.ABC – равнобедренный
3.∠ABC = 74°
Ответы
Автор ответа:
0
Ответ:
ΔABC – равнобедренный
∠ABC = 74°
AB ∥ CD
Объяснение:
1) ΔАВС - равнобедренный, так как АВ=АС
- Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им - основание.
2) CB — биссектриса ∠ACD.
∠АСВ=∠BCD = 74° - по свойству биссектрисы.
Так как в равнобедренном треугольнике углы при основании равны, то ∠АВС=∠АСВ=74°
3) ∠АВС и ∠BCD - внутренние накрест лежащие углы при прямых АВ и CD и секущей ВС. ∠АВС = ∠BCD = 74°.
- Если внутренние накрест лежащие углы равны, то прямые параллельны: AB ∥ CD
Приложения:
Похожие вопросы
Предмет: Химия,
автор: dianakerimova
Предмет: Химия,
автор: victoria46
Предмет: Русский язык,
автор: Игорь20015
Предмет: История,
автор: bururbroddik
Предмет: Литература,
автор: fopfi222222
ABC – равнобедренный треугольник
∠ABC = 74°