Предмет: Геометрия,
автор: turyginakristina13
Биссектрисы внешних углов при вершина B и C треугольника ABC пересекаются в точке O Докажите что луч AO- биссектриса угла A.
Даю 10 баллов за ответ please
Ответы
Автор ответа:
28
Ответ:
Объяснение:
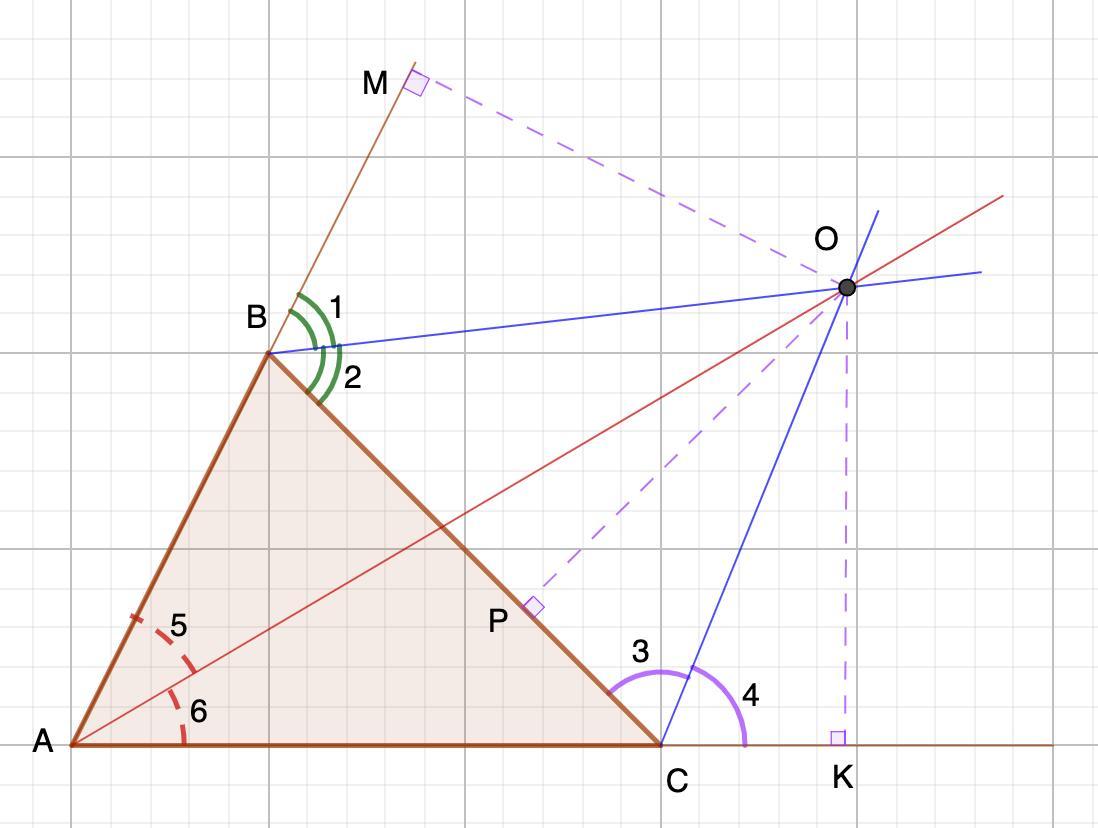
Дано: ΔАВС.
ВО - биссектриса внешнего ∠МВС;
СО - биссектриса внешнего ∠КСВ;
ВО ∩ СО=О.
Доказать: АО - биссектриса ∠А.
Доказательство:
Из точки О опустим перпендикуляры к АК, АМ и ВС.
1. Рассмотрим ΔСОК и ΔСОР - прямоугольные.
∠3=∠4 (условие)
СО - общая
⇒ ΔСОК = ΔСОР (по гипотенузе и острому углу)
⇒ ОК=ОР (как соответственные элементы)
2. Рассмотрим ΔВОР и ΔВОМ - прямоугольные.
∠1=∠2 (условие)
ВО - общая
⇒ ΔВОР = ΔВОМ (по гипотенузе и острому углу)
⇒ ОМ=ОР (как соответственные элементы)
3. ОК=ОР (п.1)
ОМ=ОР (п.2)
⇒ ОК=ОМ
4. Рассмотрим ΔАМО и ΔАОК - прямоугольные
АО - общая
ОК=ОМ (п.3)
⇒ΔАМО = ΔАОК (по катету и гипотенузе)
⇒∠5=∠6 (как соответственные элементы)
⇒АО - биссектриса ∠А.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: kaskadell
Предмет: Химия,
автор: masha990766
Предмет: Математика,
автор: 7класс2
Предмет: Биология,
автор: Alena1561786
Предмет: Математика,
автор: svarzilova