Question

Разность квадратов двух выражений. Урок 2

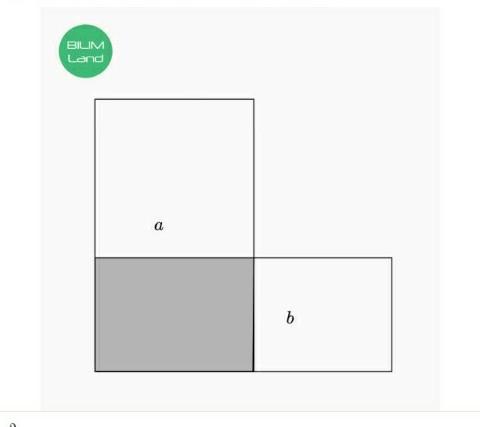
Дан прямоугольник со сторонами a и b. На его сторонах построены квадраты. Площадь одного квадрата на 21 см2 больше площади другого. Найди площадь прямоугольника, если длина прямоугольника на 3 см больше его ширины.


5 см2

7 см2

10 см2

12 см2

18 см2

​

Answer 1

Ответ:

10 см²

Объяснение:

Дано:

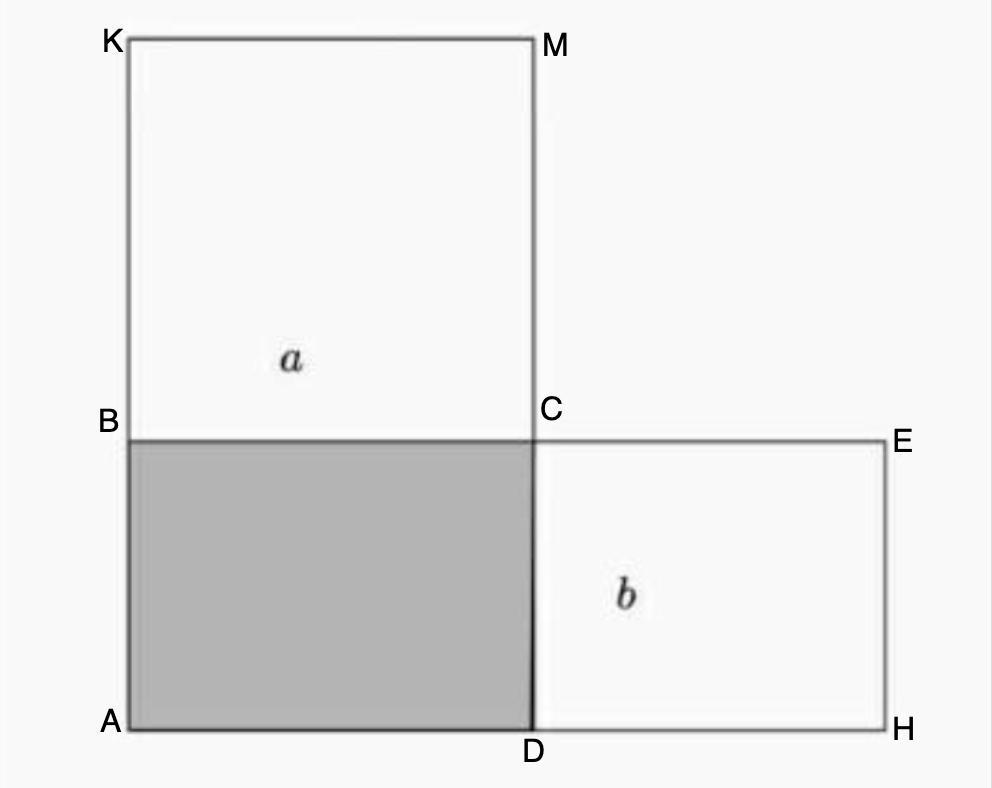
Прямоугольник ABCD.

BC = a; CD = b

BKMC и CEHD - квадраты.

S (BKMC) - S (CEHD) = 21 см²

a - b = 3 см

Найти: S (ABCD)

Решение:

a - b = 3 (см)

a = 3 + b (см)

• Площадь квадрата равна квадрату его стороны.

S (BKMC) = a² = (3 + b)²

S (CEHD) = b²

По условию:

S (BKMC) - S (CEHD) = (3 + b)² - b² = 21 (см²)

• Разность квадратов двух чисел равна произведению разности этих чисел на их сумму.

⇒ (3 + b)² - b² = (3 + b - b)(3 + b + b) = 3 * (3 + 2b) = 9 + 6b

Составим уравнение:

9 + 6b = 21

6b = 12

b = 2 (см)

⇒ а = 3 + 2 = 5 (см)

• Площадь прямоугольника равна произведению смежных сторон.

S (ABCD) = a * b = 2 *5 = 10 (см²)