Предмет: Алгебра,
автор: wemivow763
Решите уравнение пожалуйста
Приложения:
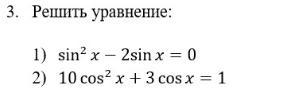
Ответы
Автор ответа:
0
Ответ:
1. x=πn, n∈N 2. x₁=-arccos(0,2)+2πn, n∈N x₂=±2π/3+2πk, k∈N
Объяснение:
1. sin²x-2sinx=0
sinx(sinx-2)=0
sinx=0; sinx-2=0
1) sinx=0
x=πn, n∈N
2) sinx=2 → x=∅, т.к. -1≤sinx≤1
Ответ: x=πn, n∈N
2. 10cos²x+3cosx=1
10cos²x+3cosx-1=0
cosx=m, m∈[-1;1]
10m²+3m-1=0
D=3²-4*10*(-1)=9+40=49=7²
m₁=(-3+7)/2*10=4/20=0,2
m₂=(-3-7)/2*10=-10/20=-0,5
cosx=0,2; cosx=-0,5
x₁=-arccos(0,2)+2πn, n∈N
x₂=±2π/3+2πk, k∈N
Похожие вопросы
Предмет: Геометрия,
автор: dashasukhanova
Предмет: Математика,
автор: eljoe
Предмет: Математика,
автор: Dashka893
Предмет: Математика,
автор: миша2606
Предмет: Литература,
автор: Alina1978123