Предмет: Математика,
автор: tvkitay
Найти градиент функции и производную по направлению
Приложения:
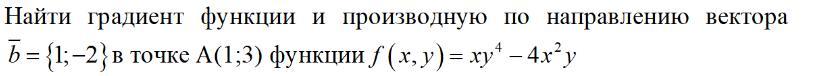
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
направление вектора-градиента задаётся его направляющими косинусами:
с градиентом покончили, теперь производная в точке А по направлению вектора b(1;-2).
направление вектора
поскольку , то заданная функция в направлении вектора b убывает.
pushpull:
и это тоже в школах проходят теперь ??????
Похожие вопросы
Предмет: Математика,
автор: veronuka48
Предмет: Математика,
автор: kirillisanbaev
Предмет: Химия,
автор: чижик68русский
Предмет: Физика,
автор: якура