Помогите пожалуйста решить. СРОЧНО Очень нужно. Буду вам очень благодарна ❤️. Нужно записать дано, решение. Нужно доказать что треугольники равны.Огромное спасибо. Очень нужно хотя бы несколько
Ответы
Ответ:
Пошаговое объяснение:
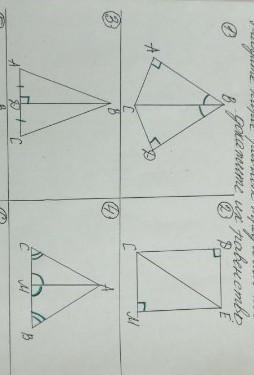
1) Дано: △ABC и △DBC. <BAC=<BDC=90°, <ABC=<DBC
Док-ть: △ABC=△DBC
Док-во: В прямоугольных тр-ках △ABC и △DBC <ABC=<DBC по условию, BC - общая гипотенуза, значит △ABC=△DBC по признаку равенства прямоуг. тр-ков:
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.
2) Я подумаю ещё, но мне кажется не хватает данных в задаче. По сути, дано что в четырёхугольнике два противоположных угла прямые, а это не говорит вообще ни о чём, по таким данным нельзя считать его прямоугольником.
3) Дано: △ABD и △CBD. AD=DC, <BDA=90°.
Док-ть: △ABD=△CBD
Док-во: Тр-ки △ABD и △CBD - прямоугольные. В них AD=DC по условию, BD - общий катет, значит △ABD=△CBD по признаку равенства прямоуг. тр-ков:
Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие прямоугольные треугольники равны.
4) Дано: △ACM и △ABM. <ACM=<ABM, <AMC=<AMB.
Док-ть: △ACM=△ABM
Док-во: Рассмотрим △ABC. В нём ACM=<ABM => △ABC - равнобедренный => AC=AB.
В △ACM <CAM=180-<ACM-<AMC, а в △ABM <BAM=180-<ABM-<AMB. Но по условию <ACM=<ABM, <AMC=<AMB, значит и <CAM=<BAM. Тогда учитывая, что AM - общая сторона этих тр-ков, делаем вывод, что △ACM=△ABM по 1-му признаку.
//*можно ещё как вариант доказать, что <AMC=<AMB, и при этом их сумма равна 180, значит каждый из них прямой. Тогда тр-ки равны по катету и острому углу.