Предмет: Геометрия,
автор: zen06kin
СРОЧНО дна из двух равных окружностей проходит через центр другой окружности.
Вычисли длину общей хорды, если радиус окружности равен 24 м.
Ответ: длина общей хорды равна
−−−−−√ м.
Ответы
Автор ответа:
4
Дано:
Окружность (O,R)
r = 24 м
-----------------------------
Найти:
AB - ?
Решение:
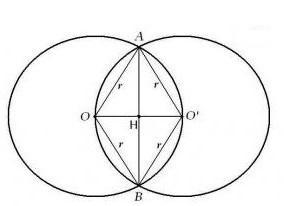
Так как AOO’B — ромб с одинаковой диагональю равно радиусу окружности , то есть OO’=r=24 м
В равностороннем ΔOAO’, а AH-высота, следовательно мы можем найти высоту по такой формуле:
AH = (r√3)/2 = 24√3 м/2 = 12√3 м ⇒ AH = BH = 12√3 м
И теперь мы находим общую хорду AB:
AB = AH + HB = 12√3 м + 12√3 м = 24√3 м
Ответ: AB = 24√3 м
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Olesya345
Предмет: Математика,
автор: kypruxinevgenii
Предмет: Русский язык,
автор: 1olen
Предмет: Геометрия,
автор: prohorenkova1
Предмет: Математика,
автор: fvfhcdfcb