Предмет: Математика,
автор: ange1787
Срочно пожалуйста отправляйте
Приложения:
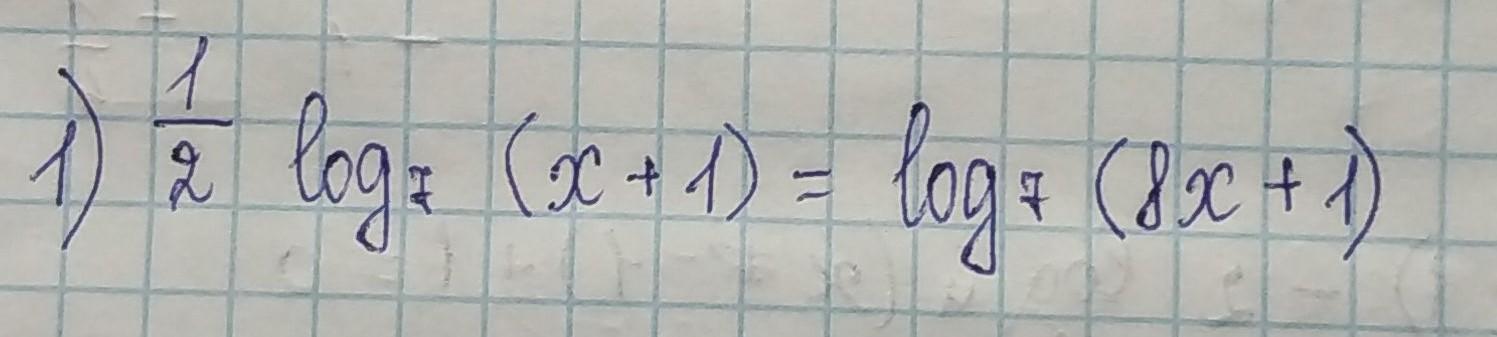
Ответы
Автор ответа:
1
Проверка корней:
Получилось верное равенство, число 0 является решением уравнения.
Выражение под логарифмом не может быть отрицательным. Значит, число (-15/64) решением уравнения не является.
Ответ: 0.
Похожие вопросы
Предмет: Русский язык,
автор: рег1
Предмет: Физика,
автор: alxlie1999
Предмет: Русский язык,
автор: yarik20156
Предмет: Геометрия,
автор: kartes2514
Предмет: Математика,
автор: настя7063