Предмет: Геометрия,
автор: anelya3822
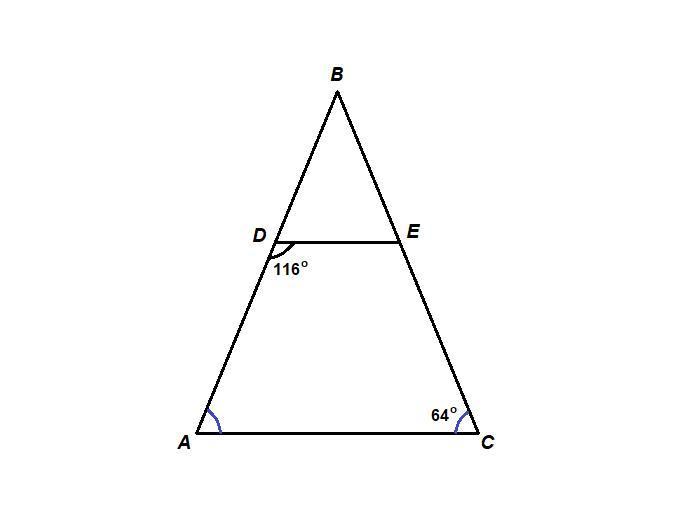
В треугольнике ABC стороны AB = CB. Точки D и E взяты на сторонах AB и CB соответственно. Если ∠ADE = 116°, ∠ACE = 64°, докажи, что прямые DE и AC параллельны.
Заполни пропуски:
Так как по условию задачи AB = CB, то треугольник ABC –
треугольник. По свойству равнобедренного треугольника ∠BAC = ∠BCA =
.
Углы DAC и ADE — это углы
, когда прямые DE и AC пересекаются третьей прямой
. По
признаку параллельности прямых прямые DE и AC параллельны, так как ∠DAC +
= 64° + 116° = 180°.
помогите пожалуйста
дам 40 баллов за правильный ответ!!!
Ответы
Автор ответа:
3
Ответ:
Так как по условию задачи AB = CB, то треугольник ABC – равнобедренный треугольник.
По свойству равнобедренного треугольника ∠BAC = ∠BCA = 64°.
Углы DAC и ADE — это углы внутренние односторонние, которые образуются, когда прямые DE и AC пересекаются третьей прямой АВ. По третьему признаку параллельности прямых прямые DE и AC параллельны, так как
∠DAC + ∠ADE = 64° + 116° = 180°.
Приложения:
Похожие вопросы
Предмет: Биология,
автор: rogovayakatya
Предмет: Українська мова,
автор: Maximenkovlad
Предмет: Русский язык,
автор: рег1
Предмет: Математика,
автор: rufatruslan1
Предмет: Обществознание,
автор: litvintsevagp6