Question

Решение текстовых задач с помощью квадратных уравнений
Найди стороны прямоугольника, если периметр прямоугольника равен 18 см, а его диагональ -
$\sqrt{53}$
см.
Ответ запиши в порядке убывания.
Ответ: ?см; ?см.

​

Answer 1

Ответ:

7 см; 2 см.

Объяснение:

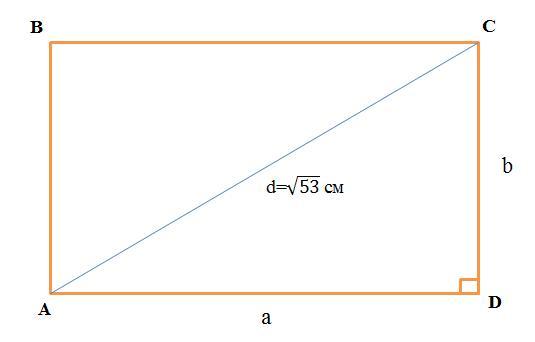
Дано (см. рисунок):

  Прямоугольник ABCD

  a=AD=BC - длина

  b=AB=CD - ширина

  P(ABCD)=18 см

  d=AC=$\sqrt{53}$ см  

Найти: a и b.

Решение.

Периметр прямоугольника со сторонами a и b равен:

P(ABCD) = 2·(a + b).

Значит:

2·(a + b) = 18 или a + b = 9 или a = 9 - b.

В прямоугольном треугольнике ACD верна теорема Пифагора:

d² = a² + b².

Тогда

a² + b² = $(\sqrt{53})^2$ или a² + b² = 53

Подставим выражение для a = 9 - b в последнее уравнение и решим:

(9 - b)² + b² = 53

b² - 18·b + 81 + b² - 53 = 0

2·b² - 18·b + 28 = 0

b² - 9·b + 14 = 0

D = (-9)² - 4·1·14 = 81 - 56 = 25 = 5²,

b = (9-5)/2 = 2 см, то a = 9 - 2 = 7 см - подходит, так как в прямоугольнике длина должен быть больше чем ширина

b = (9+5)/2 = 7 см, то a = 9 - 7 = 2 см - не подходит по той же причине.