Предмет: Геометрия,
автор: kusainovi
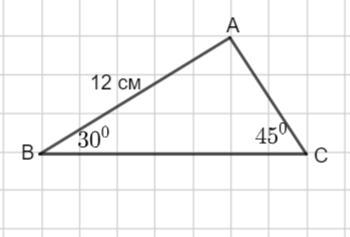
Дан треугольник ABC. Если AB = 12 см, ∠B = 30° и ∠C =45°, то найди длину стороны AC.
Ответ:
Ответы
Автор ответа:
4
Ответ:
AC= 6√2 см.
Объяснение:
Рассмотрим Δ АВС .
∠В=30°, ∠С=45° , АВ= 12 см.
Воспользуемся теоремой синусов: стороны треугольника пропорциональны синусам противолежащих углов.
AC= 6√2 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: DashaF2000
Предмет: Биология,
автор: Xamachi
Предмет: Математика,
автор: olishkaolia84
Предмет: Литература,
автор: Sasha1862