Question

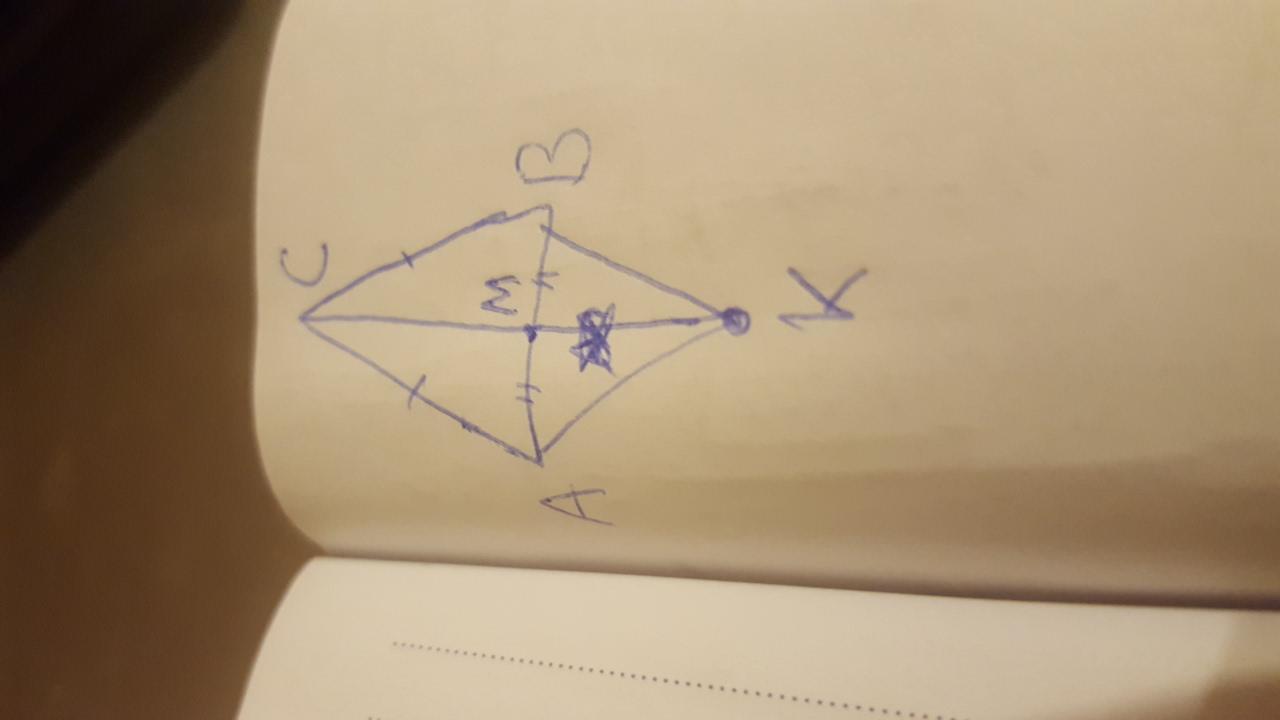
В равнобедренном треугольнике ABC с основанием AB проведена медиана CM. На продолжении медианы за точку M взята точка K. Докажите что треугольники AMK и BMK равны.

Answer 1

Ответ:

Объяснение:

Т.к. СМ- медиана, проведенная из угла равнобедренного треугольника, лежащего напротив основания, то она является одновременно и бисектрисой и высотой для него

Исходя из свойств перпендикулярных прямых, можно сказать, что <AMK=<BMK=90º

Также сторона КМ у треугольников АМК и ВМК общая

АМ=МВ по условию (ведь СМ- медиана)

Таким образом треугольники АМК и ВМК равны по двум сторонам и углом между ними