Предмет: Математика,
автор: gintsveveris
Pozalujsta pomogite. Ocen nada segodnja. Pozalujsta. VTorije foto naidite proizvodnuju. Ocen ocen nada.
Приложения:
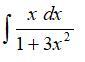
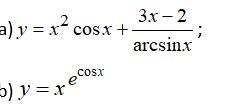
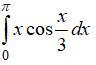
Ответы
Автор ответа:
4
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Математика,
автор: staffegor
Предмет: Русский язык,
автор: татьянамедведева
Предмет: Другие предметы,
автор: инфинитив
Предмет: Алгебра,
автор: TyTToŪLLlkoJlbHuK
Предмет: Математика,
автор: Nastya24052004