Предмет: Алгебра,
автор: sashaenique88
Розв’яжіть нерівність ≥ 4х-1.
Приложения:
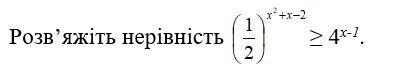
Ответы
Автор ответа:
1
Ответ:
⇒
x ∈ [-4; 1]
⇒
x ∈ ∅
Ответ: x ∈ [-4; 1]
Похожие вопросы
Предмет: Биология,
автор: MBmagic
Предмет: Математика,
автор: bekmametovaeli
Предмет: Литература,
автор: olgatitova79
Предмет: Математика,
автор: Kqv
Предмет: Математика,
автор: рагимовРинат