Предмет: Математика,
автор: Grigoiy
Пожалуйста, решите эти задания. Желательно с объяснениями.
Приложения:
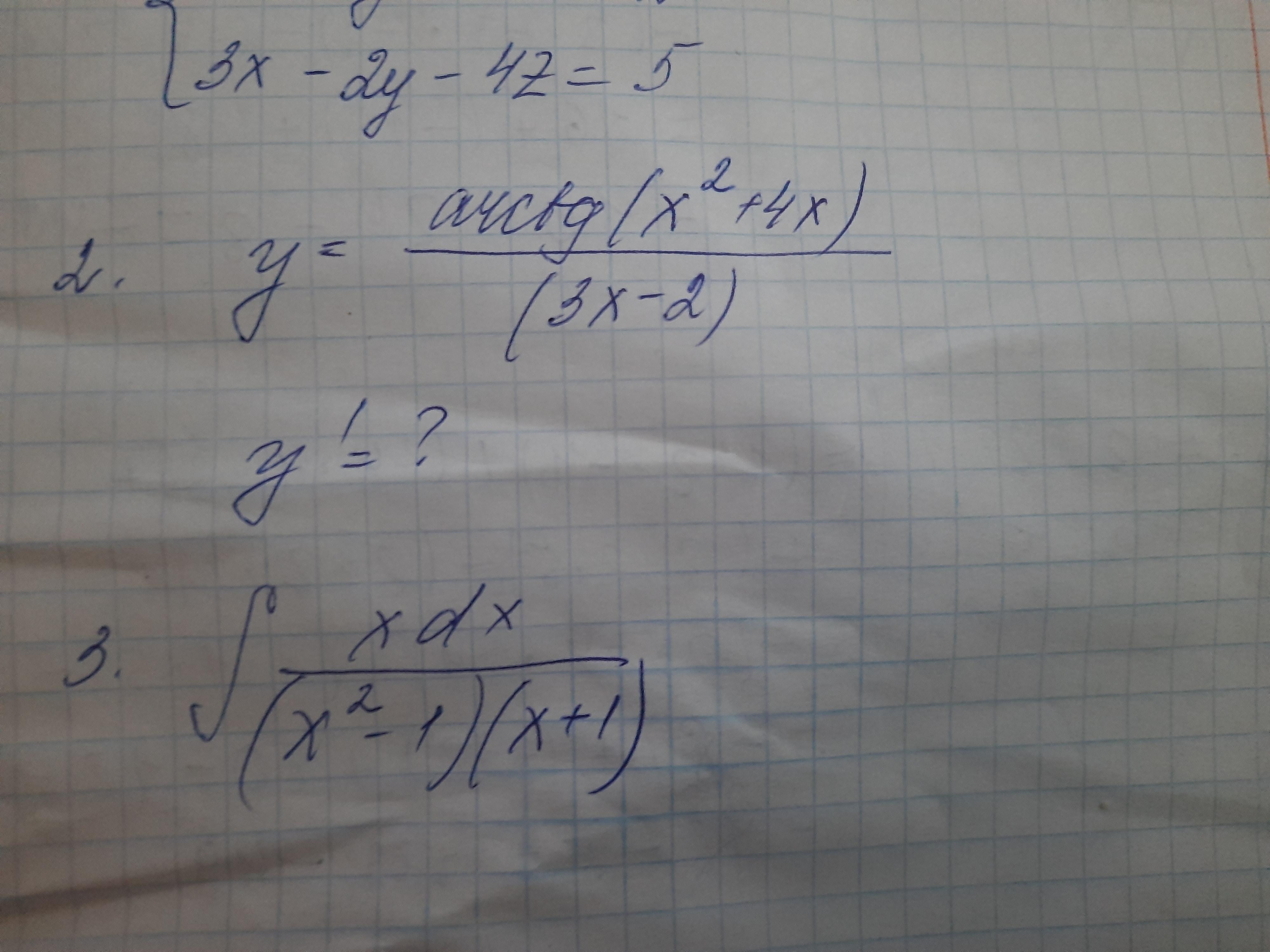
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
2
3
метод разложения на простейшие
A(x+1)² +B(x-1)(x+1)+C(x-1)=x
x²: A + B = 0
x: 2A + C = 1
1: A -B -C = 0
Решая ее, находим:
A = 1/4; B = -1/4; C = 1/2;
и вот получим
Похожие вопросы
Предмет: Математика,
автор: olgazhuravleva2
Предмет: Литература,
автор: juliajulia02
Предмет: Алгебра,
автор: lizasavenkova
Предмет: Математика,
автор: ema87
Предмет: Математика,
автор: Hjhghk