Предмет: Математика,
автор: Natali23458
Помогите с математикой пожалуйста!!!
Приложения:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
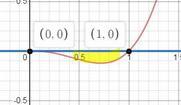
рисуем график и находим на нем пределы интегрирования
интегрируем по частям
f = lnx; ⇒ f' = 1/x
g' = x³; ⇒ g= x⁴/4
здесь получается функция
но lnx в точке х₀=0 терпит разрыв. поэтому вместо f*g мы будем рассматривать предел.
и вот
вычислим предел
тогда
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: bykovanika2004
Предмет: География,
автор: sofikovfvf20021
Предмет: Биология,
автор: Ликанна
Предмет: Математика,
автор: d1mon11
Предмет: Алгебра,
автор: Sofiya030701