Предмет: Геометрия,
автор: ksyuta05
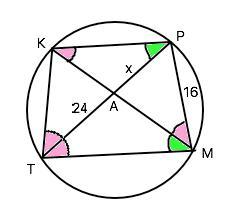
В выпуклом четырёхугольнике MPKT диагональ TP является биссектрисой угла MTK и пересекается с диагональю MK в точке A. Найдите AP, если известно, что около четырёхугольника MPKT можно описать окружность, МР=16, АТ=24. Даю 30 баллов.
Ответы
Автор ответа:
11
Ответ: АР=8
Объяснение (подробно):
ТР - биссектриса ⇒ ∠КТР=∠РТМ.
Т.к. около четырехугольника описана окружность, все углы, вершины которых лежат на ней, -вписанные. Вписанные углы, которые опираются на одну дугу, равны; равны и хорды, которые стягивают равные дуги.
Угол РМК опирается на дугу РК, и угол КТР опираются на дугу КР, следовательно они равны. Но им равен и угол РТМ , следовательно, равны хорды КР=РМ=16.
Примем АР=х. Тогда ТР=ТА+х=24+х
Рассмотрим ∆ ТКР и АКР. Они имеют по два равных угла, следовательно, подобны. Из их подобия следует отношение ТР:КР=КР:АР ⇒
(24+х):16=16:х
Из пропорции получаем 14х+х²=256 ⇒ х²+24х-256. Решив квадратное уравнение находим х₁=8; х₂=-32 ( не подходит).
АР=х=8.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: bazarova1082002
Предмет: Русский язык,
автор: buran2006
Предмет: Русский язык,
автор: ninzyaznani555
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним