Question

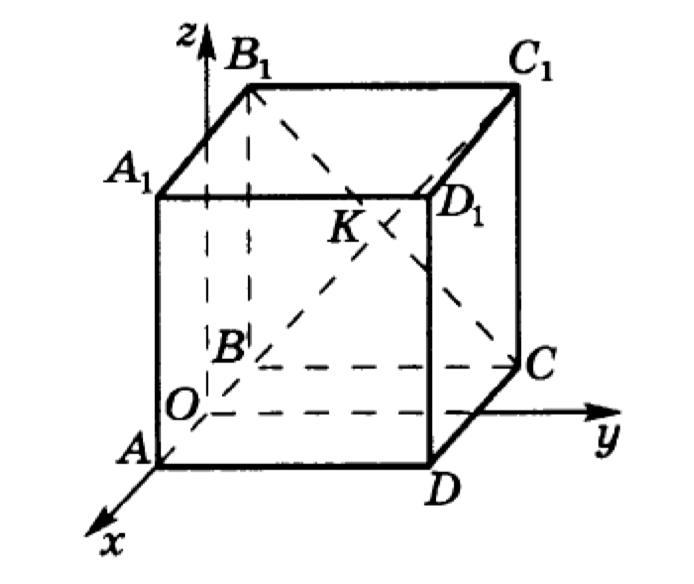
Куб ABCDA1B1C1D1 помещён в прямоугольную систему координат (см. рисунок), O – середина ребра AB, С(-2;4;0).


а) Найдите координаты всех остальных вершин куба.


б) Найдите координаты векторов OC, OB1 и OK и разложите их по координатным векторам i, j и k.

Answer 1

Дано:

ABCDA₁B₁C₁D₁ - куб

O – середина ребра AB

С(-2;4;0)

------------------------------------------

Найти:

а) Найдите координаты всех остальных вершин куба.

б) Найдите координаты $\overrightarrow{OC}, \overrightarrow{OB_{1}} , \overrightarrow{OK}$

Решение:

а) Из условия задачи мы знаем что С(-2;4;0), значит что ребра этой кубы всего будет 4, отсюда мы получаем координаты всех остальных вершин куба:

A(2;0;0); B(-2;0;0); D(2;4;0); A₁(2;0;4); B₁(-2;0;4); C₁(-2;4;4); D₁(2;4;4)

б) Допустим у нас точка О — является началом координат. Чтобы вычислить координаты вектора, зная координаты (x₁; y₁) его начала A и координаты (x₂; y₂) его конца B, нужно из координат конца вычесть координаты начала: (x₂-x₁; y₂-y₁).

На этом рисунке мы имеем точки с координатами О(0;0;0), С(-2;4;0), В₁(-2;0;4) и K (-2;2;2). Из этого следует:

$\overrightarrow{OC} (-2-0;4-0;0-0)\Rightarrow \overrightarrow{OC} (-2,4,0) \Rightarrow \overrightarrow{OC} = -2 \vec i + 4 \vec j + 0 \vec k$

$\overrightarrow{OB_{1}} (-2-0;0-0;4-0)\Rightarrow \overrightarrow{OB_{1}} (-2,0,4) \Rightarrow \overrightarrow{OB_{1}} = -2 \vec i + 0 \vec j + 4 \vec k$

$\overrightarrow{OK} (-2-0;2-0;2-0)\Rightarrow \overrightarrow{OK} (-2,2,2) \Rightarrow \overrightarrow{OK} = -2 \vec i + 2 \vec j + 2 \vec k$

(K - середина BC₁ и B₁C ⇒ K(-2,2,2))

Ответ: а) A(2;0;0); B(-2;0;0); D(2;4;0); A₁(2;0;4); B₁(-2;0;4); C₁(-2;4;4); D₁(2;4;4)

б) $\overrightarrow{OC} = -2 \vec i + 4 \vec j + 0 \vec k$ ; $\overrightarrow{OB_{1}} = -2 \vec i + 0 \vec j + 4 \vec k$ ; $\overrightarrow{OK} = -2 \vec i + 2 \vec j + 2 \vec k$

Решено от : $DK954$