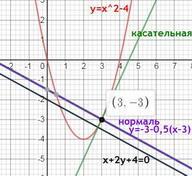
Нужно провести нормаль к функции y=x^2-4х параллельно прямой х+2y+4=0 .Сделать чертеж .
Даю 100 баллов за срочность
Ответы
Ответ:
Пошаговое объяснение:
сперва перепишем х+2y+4=0 в виде уравнения с угловым коэффициентом
y = -0.5x-2
здесь коффициент угла наклона = -0,5
значит, у нашей нормали должен быть такой же коффициент угла наклона = -0,5
значит ⇒ y'(x₀)=2
y'(x) = 2x-4; 2x₀-4=2; x₀ = 3; у(х₀) = 3²-4*3=9-12 = -3
вот в этой точке (3; -3)и будет проходить нормаль к графику
а уравнение нормали
теперь проверим. напишем касательнуб в этой точке
и проверим, что они перепендикулярны
направляющий вектор нормали n₁ = (1; -05)
направляющий вектор касательной n₂ = (1; 2)
их скалярное произведение
a · b = ax · bx + ay · by = 1 · 1 + (-0.5) · 2 = 1 - 1 = 0
Так как скалярное произведение равно нулю, то эти векторы перпендикулярны
т.е. мы правильно нашли точку и построили в ней нормаль параллельную х+2y+4=0