Question

Помогите пожалуйста, никак не могу решить

Answer 1

Ответ:

Пошаговое объяснение:

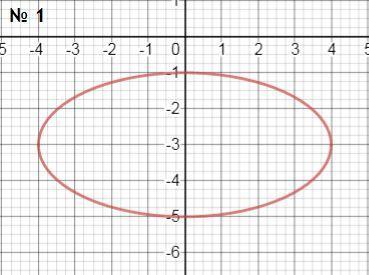
1)

$x=-2\sqrt{-5-6y-y^2}$

сначала избавимся от радикала

получим x²+4y²+24y+20=0

Приводим квадратичную форму:

B = x² + 4y²

к главным осям, то есть к каноническому виду.

матрица этой квадратичной формы:

1   0

0   4

теперь  собственные числа и собственные векторы этой матрицы:

(1 - λ)*х₁ + 0*y₁ = 0

0*x₁ + (4 - λ)y₁ = 0

xарактеристическое уравнение:

$\left[\begin{array}{ccc}1-\lambda&0\\0&4-\lambda\\\end{array}\right] =\lambda^2-5\lambda+4=0$

λ² -5 λ + 4 = 0    ⇒  λ₁ = 4;   λ₂ = 1

исходное уравнение определяет эллипс (λ₁ > 0; λ₂ > 0)

Вид квадратичной формы:

x² + 4y²

4(y²+2*3y + 32) -4*32 = 4(y+3)²-36

Разделим все выражение на 16

и получим каноническое уравнение исходного эллипса. однако, вспомним, что мы возводили исходное выражение в квадрат, поэтому мы фактически добавили "правый полуэллипс". поэтому у на будет ограничение x ≤0

$\frac{1}{16} x^2+\frac{1}{4} (y+3)^2=1;$   для $x \leq 0$

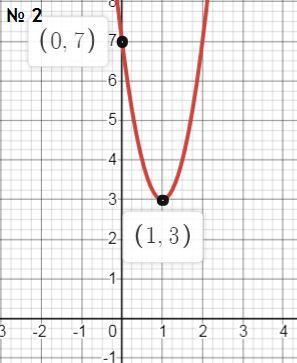
2) y = 4x² -8x +7

преобразуем

4x² -8x +7 - у = 0

приводим квадратичную форму:

B = 4x²

к главным осям, то есть к каноническому виду.

матрица этой квадратичной формы:

4   0

0    0

находим собственные числа и собственные векторы этой матрицы:

(4 - λ)x₁ + 0*y₁ = 0

0*x1 + (0 - λ)*y₁ = 0

характеристическое уравнение:

λ2 -4 λ + 0 = 0  ⇒  λ₁=4     λ₂=0

исходное уравнение определяет параболу (λ₂ = 0)

Вид квадратичной формы:

4x²

Выделяем полные квадраты:

для x:

4(x²-2*1x + 1) -4*1 = 4(x-1)²-4

преобразуем и получим

$(x-1)^2=\frac{1}{4} (y-3)$

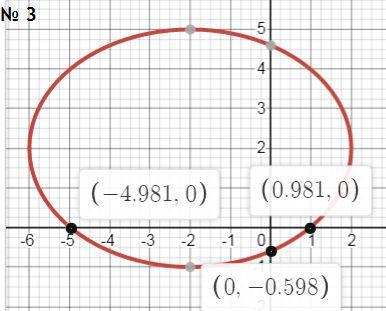
3)

9x²+16y²+36x-64y-44=0

приводим квадратичную форму:

B = 9x² + 16y²

к главным осям, то есть к каноническому виду.

матрица этой квадратичной формы:

9    0

0     16

находим собственные числа и собственные векторы этой матрицы:

(9 - λ)x₁ + 0*y₁ = 0    

0*x₁ + (16 - λ)y₁ = 0

характеристическое уравнение:

λ² -25 λ + 144 = 0  ⇒  λ₁ =16        λ₂=9

исходное уравнение определяет эллипс (λ1 > 0; λ2 > 0)

вид квадратичной формы:

9x² + 16y²

выделяем полные квадраты:

для x:

9(x1²+2*2x + 22) -9*2² = 9(x+2)²-36

для y:

16(y²-2*2y + 22) -16*2² = 16(y-2)²-64

В итоге получаем:

9(x+2)²+16(y-2)² = 144

Разделим все на 144, получим

$\frac{1}{16} (x+2)^2+\frac{1}{9} (y-2)^2=1$