Предмет: Алгебра,
автор: Vladtiger
помогите пожалуйста, срочно нужно!!
Приложения:
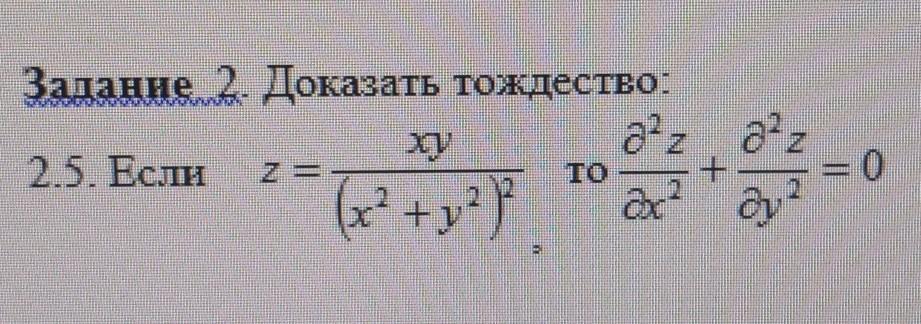
Ответы
Автор ответа:
1
Ответ:
в равенство подставляем:
чтд.
Похожие вопросы
Предмет: Математика,
автор: lissenokk
Предмет: Математика,
автор: hacer342
Предмет: Русский язык,
автор: иносҭϷаԋочӄ
Предмет: Информатика,
автор: Наночкка
Предмет: Математика,
автор: Malıw