Предмет: Математика,
автор: nataliazyateva
ПОМОГИТЕ СРОЧНО!!!!!!
Помогите пожалуйста решить неопределённые интегралы, обязательно с подробным интегрированием
Приложения:
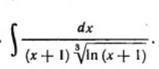
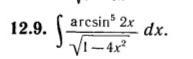
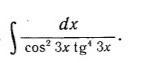
Ответы
Автор ответа:
1
Ответ:
1.
1/(x+1) - это производная логарифма, заносим под знак дифференциала
2.
1/(1-4x^2)^(1/2)) - это производная акрсинуса. Заносим под дифференциал, но сначала добавим в него двойку, так как функция сложная.
3.
1/cos^2x - производная тангенса. Заносим под дифференциал, но сначала добавим 3.
Похожие вопросы
Предмет: Русский язык,
автор: LinaZhuldikova
Предмет: Английский язык,
автор: chibnetuser
Предмет: Обществознание,
автор: 530311530287
Предмет: Математика,
автор: ГвоЗдиик
Предмет: Литература,
автор: azizjonmurotov