Предмет: Геометрия,
автор: porrige2015
Из точки, находящейся на расстоянии 8 см от плоскости, проведена к плоскости наклонная, которая образует с плоскостью угол 45°. Найдите длину плоскости.
porrige2015:
Все, что я знаю, это то что в ответе должно получиться что-то с корнем(
Длину плоскости найти невозможно, вы что-то напутали.
тогда скорее всего нужно найти длину наклонной
Ответы
Автор ответа:
0
Ответ:
8
Объяснение:
я так понимаю, это решается вот как
так как расстояние до плоскости определяется, высотой опущенной на плоскость.
значит получаем прямоугольник с углом в 45 градусов и 90
третий угол равен 180-90-45=45
это значит равнобедренный треугольник
следует длина плоскости равна высоте (восьми)
Автор ответа:
1
Требуется найти длину наклонной.
Ответ:
4√8 см.
Объяснение:
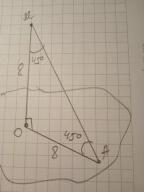
Дано: плоскость α; МО⊥α; МО=8 см. ∠ОАМ=45°. Найти АМ.
ΔОАМ - прямоугольный, ∠М=∠А=45°, т.к. сумма острых углов прямоугольного треугольника составляет 90°. Значит ОА=ОМ=8 см.
По теореме Пифагора АМ=√(ОМ²+ОА²)=√(64+64)=√128=4√8 см.
Приложения:
8√2
оба ответа верны
Похожие вопросы
Предмет: Математика,
автор: Denis982
Предмет: Биология,
автор: ananaCik22
Предмет: Математика,
автор: vika1234000
Предмет: Математика,
автор: Kesalavreshina
Предмет: Математика,
автор: fara36