Предмет: Математика,
автор: juliaelesova
Решить неопределенный интеграл
Приложения:
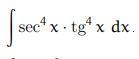
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: Milaska193
Предмет: Биология,
автор: snezhanaporohny
Предмет: Английский язык,
автор: Квилетова
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: аля353545