Предмет: Математика,
автор: juliaelesova
Решить неопределенный интеграл
Приложения:
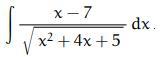
Ответы
Автор ответа:
1
Ответ:
производная знаменателя:
делаем ее в числителе:
Похожие вопросы
Предмет: Математика,
автор: karpik1вася
Предмет: Математика,
автор: TheMakerX
Предмет: Математика,
автор: Swager1
Предмет: Математика,
автор: 4Дарья2