Предмет: Геометрия,
автор: vasyakasym06
На двух противоположных сторонах параллелограмма взяли две точки так, что отмеченные отрезки равны. Докажите, что соединяющий эти точки отрезок делится показанной диагональю параллелограмма пополам.
(Пожалуйста с объяснением)
Приложения:
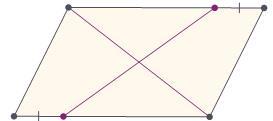
ViktoriaPobloki:
полученные треугольники равны, а эти отрезки - соответственные элементы в них
Ответы
Автор ответа:
4
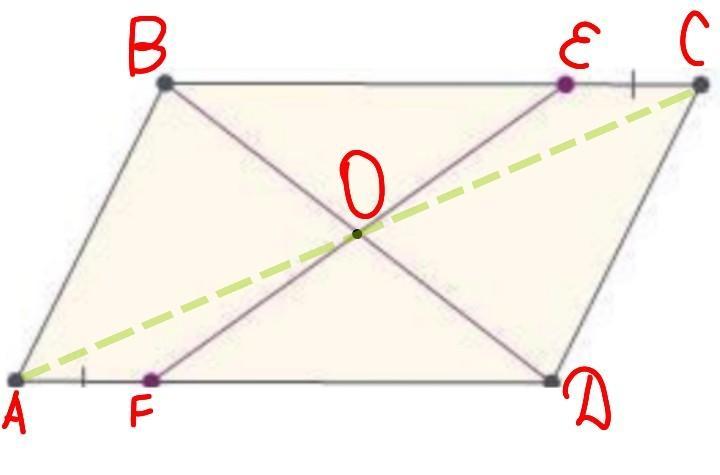
Возможно, я как-то усложнила решение задачи, просто это первое, что мне в голову пришло, но это точно правильно)
Итак:
Дано:
ABCD - параллелограмм;
BD - диагональ;
(.)E ∈ BC;
(.)F ∈ AD;
EC = AF
Доказать: FO = OE
Доказательство:
Проведём диагональ AC:
!!! △AOF и △EOC:
BC || AD; AC - секущая:
∠OAF = ∠OCE (т.к. они накрест лежащие)
BC || AD; FE - секущая:
∠OFA = ∠OEC (т.к. они накрест лежащие)
EC = AF (по условию)
=> △AOF =△EOC (по II признаку равенства△) => OC = OA; FO = OE
ч.т.д.
Приложения:
усложнила, но совсем немного)
Лео на аве здоровье маме
kakenasylym, ))
Похожие вопросы
Предмет: Математика,
автор: KirillSomenko
Предмет: География,
автор: нал1
Предмет: Русский язык,
автор: kitsan11
Предмет: Математика,
автор: Алина140506