Не могу решить задачу Помогите!
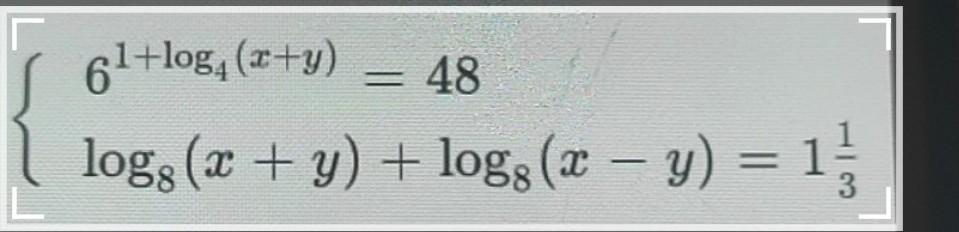
Ответы
log(8) ( x + y) + log(8) ( x - y) = 1 1/3
одз x + y > 0 x - y > 0
log(8) (x + y)(x - y) = log(8) 8^4/3
(x + y)(x - y) = 16
6^(1 + log(4) ( x + y)) = 48
6*6^log(2) √(x + y) = 6*8
x ^ log(y) z = y^ log(x) z
2^log(6) √(x + y) = 2^3
log(6) √(x + y) = 3
√(x + y) = 6^3
x + y = 6^6
x - y = 16/6^6
2x = 6^6 + 16/6^6
x = (6^6 + 16/6^6)/2
y = (6^6 - 16/6^6)/2
Відповідь:
x=4.099494563
y=0.8976946457
Покрокове пояснення:
log_8 (x+y)+log_8 (x-y) = 1/3log_2 (x+y)+1/3log_2 (x-y)=4/3
log_2 (x+y)+log_2 (x-y)=4
log(x^2-y^2)=log_2(2^4)
x^2-y^2=16
6^(log_4(x+y)=8
(6^(log_2(x+y))^(1/2)=8
6^(log_2(x+y)=64
log_6(6^(log_2(x+y)) =log_6 (64)
log_2(x+y)=6/log_2(6)=2.3211168434
Подставим в предидущее уравнение
log_2 (x+y)+log_2 (x-y)=4
log_2 (x-y)=4-2.3211168434=1.678883156
x-y=2^1.678883156
x-y=3.201799918
x=y+3.201799918
Подставим x в
x^2-y^2=16
(y+3.201799918)^2-y^2=6.403599836y+10.251522714=16
y=0.8976946457
Подставим y в x=y+3.201799918
x=0.8976946457+3.201799918
x=4.099494563