Предмет: Математика,
автор: Аноним
Задание 5. Решите систему линейных уравнений методом Крамера
Приложения:
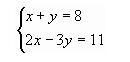
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Запишем и вычислим главный определитель системы.
Элементами главного определителя являются коэффициенты при переменных "х" и "у":
Главный определитель не равен нулю ⇒ система совместна.
Запишем и вычислим первый вспомогательный определитель. Для этого заменим первый столбец на столбец свободных членов:
Запишем и вычислим второй вспомогательный определитель. Для этого заменим второй столбец на столбец свободных членов:
Переменные "х" и "у" находятся по следующей формуле:
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: milise
Предмет: Математика,
автор: ангелочек31
Предмет: Математика,
автор: golubes
Предмет: Математика,
автор: liliyamashrabova
Предмет: Математика,
автор: Улия1111