Предмет: Алгебра,
автор: testtestovyi2020
Найти производные dy/dx функции
Приложения:
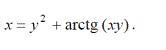
Ответы
Автор ответа:
0
Ответ.
Похожие вопросы
Предмет: Русский язык,
автор: zmelbnikof2015
Предмет: Математика,
автор: sneshana1
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Рамзан2006
Предмет: Математика,
автор: VaReNiK37