Предмет: Алгебра,
автор: testtestovyi2020
Найти производную функции с описанием шагов
Приложения:
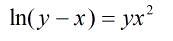
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Відповідь:
Пояснення:
Проинтегрируем бе части уравнения
1/(у-х)×(у'-1)=2ху+у'х^2
у'(1/(у-х) -х^2) = 2ху+1/(у-х)
у'=(2ху(у-х)+1)/ (1-(у-х)×х^2)
Похожие вопросы
Предмет: Математика,
автор: Гелка1
Предмет: География,
автор: mariadubok
Предмет: Алгебра,
автор: shuraefremova
Предмет: Математика,
автор: bog33451
Предмет: Математика,
автор: Sonechka2222222222