Предмет: Алгебра,
автор: sobakazabiyaka
Вычислить несобственный интеграл и установить расходимость

Ответы
Автор ответа:
0
------------------------
Приложения:
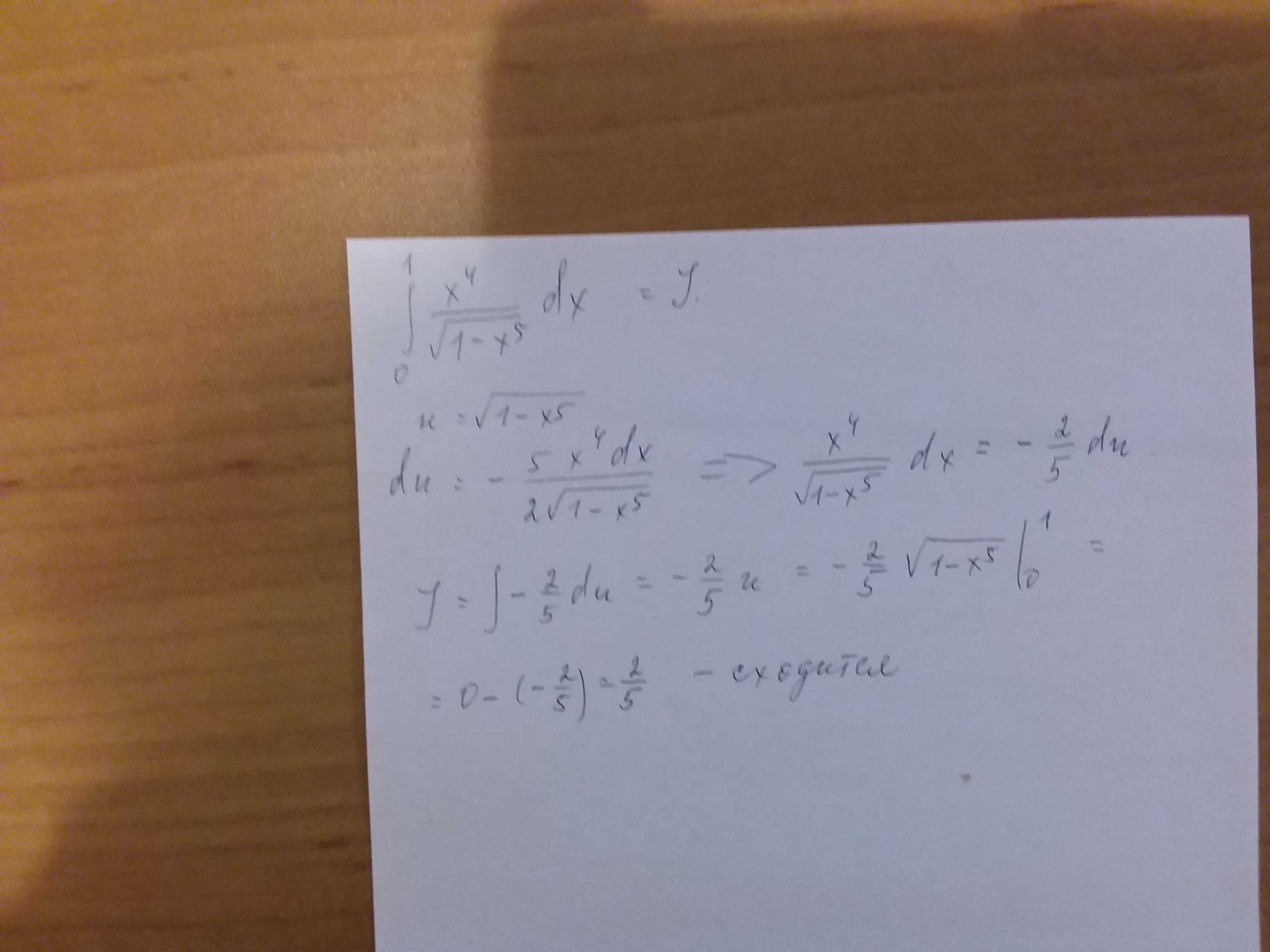
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: История,
автор: шурраr
Предмет: Математика,
автор: ulianaiana86
Предмет: Математика,
автор: Даша346
Предмет: Математика,
автор: raf1988r