Предмет: Алгебра,
автор: nparamonov2
Границы и производные
Приложения:

dasasysikova:
а на русском
4. Вычислите границу по правилу Лопиталя:
5.Найдите в точке М (1; 1), если
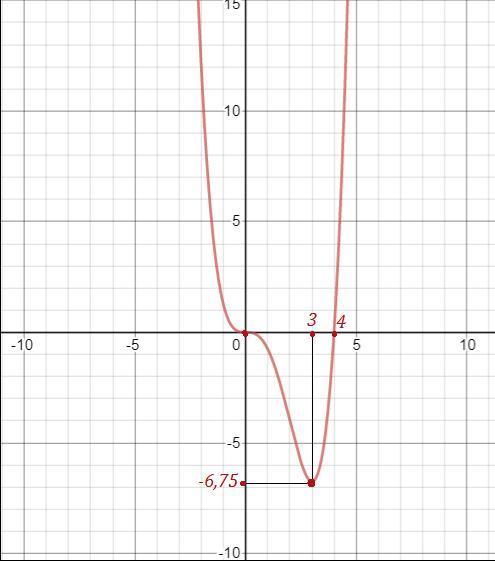
6. Найдите экстремум функции и постройте ее график.
5.Найдите в точке М (1; 1), если
6. Найдите экстремум функции и постройте ее график.
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Артур998
Предмет: Геометрия,
автор: danya1ytu
Предмет: Алгебра,
автор: kub999
Предмет: Математика,
автор: МатвейБазылев228
Предмет: Математика,
автор: Аноним