Предмет: Алгебра,
автор: nparamonov2
Границы и производные, 40 балов.
Приложения:
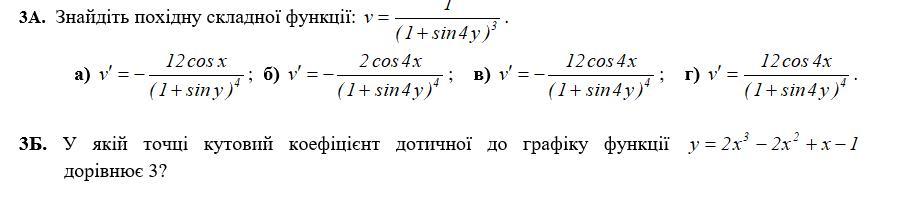
NNNLLL54:
dвсе ответы в задании 3А неверные, т.к. они содержат "х" , которого в записи функции не было ...
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: kub999
Предмет: Математика,
автор: vadimnikolas
Предмет: Математика,
автор: ulianaiana86
Предмет: Математика,
автор: Вика12345678909