Предмет: Математика,
автор: duisalievasabina
используя формулы синуса, косинуса, тангенса, котангенса суммы и разности двух углов, а также формулы двойных углов упростить выражение. буду очень признательна за подробное решение. спасибо!
Приложения:
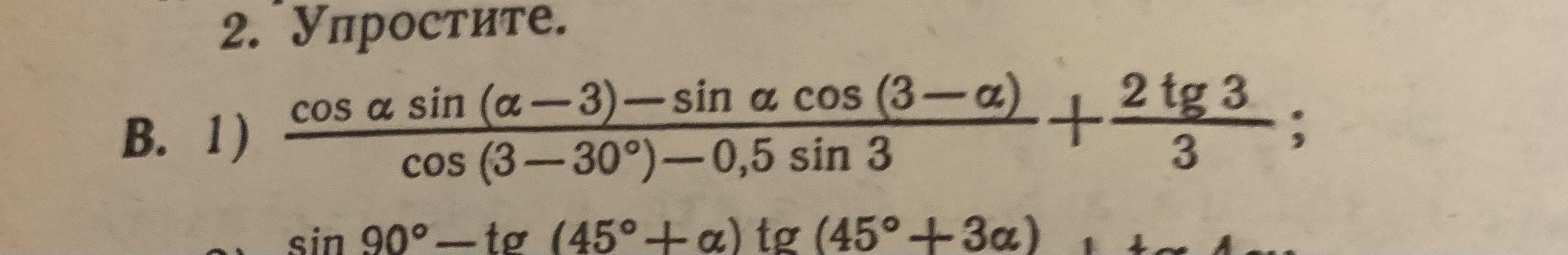
Ответы
Автор ответа:
1
1) Числитель первой дроби (синус разности):
2) Знаменатель первой дроби (косинус разности):
3) Первая дробь ():
4)
Ответ:
duisalievasabina:
спасибо вам большое!
Похожие вопросы
Предмет: Литература,
автор: ghuseynova1998
Предмет: Английский язык,
автор: Кэмка1
Предмет: Математика,
автор: веескела
Предмет: Математика,
автор: вероника1079
Предмет: Алгебра,
автор: Аноним