Предмет: Алгебра,
автор: happyms
Вычислить пределы функции c разъяснениями
Приложения:
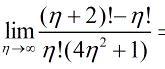
Ответы
Автор ответа:
0
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: lerochka2494
Предмет: Математика,
автор: Марфуням
Предмет: Биология,
автор: seryugggvssc
Предмет: Физика,
автор: olenkashubina15