Question

В прямоугольном треугольнике катеты относятся как 3:2, а высота де
лит гипотенузу на отрезки, из которых один на 2 см больше другого.
Найти длины сторон треугольника.

Answer 1

Ответ: 1,6 см;  3,6 см; 5,2 см.

Объяснение:

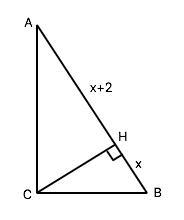
   Назовём треугольник АВС; угол С=90°, АС:СВ=3:2, АН=ВН+2.

Примем ВН=х, АН=х+2.

Каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу: ⇒

АС²=АВ•АН=(х+х+2)•(х+2)=2•(х+1)•(х+2)

ВС²=АВ•ВН=(х+х+2)•х=2•(х+1)•х

По условию АС:ВС=3:2 => АС²:ВС²=3²:2²= 9:4

Подставим найденные выше значения катетов в пропорцию:

2•(х+1)•(х+2):2•(х+1)•х=9:4⇒

(х+2):х=9:4

5х=8 ⇒

BH=х=1,6

AН=1,6+2=3,6 см

АВ=2х+2=5,2 см

АС=√(5,2•3,6)=6√52

BC=√(5,5•1,6)=4√52