Предмет: Геометрия,
автор: zeynebhashimli7
ПРОШУ ПОМОГИТЕ!
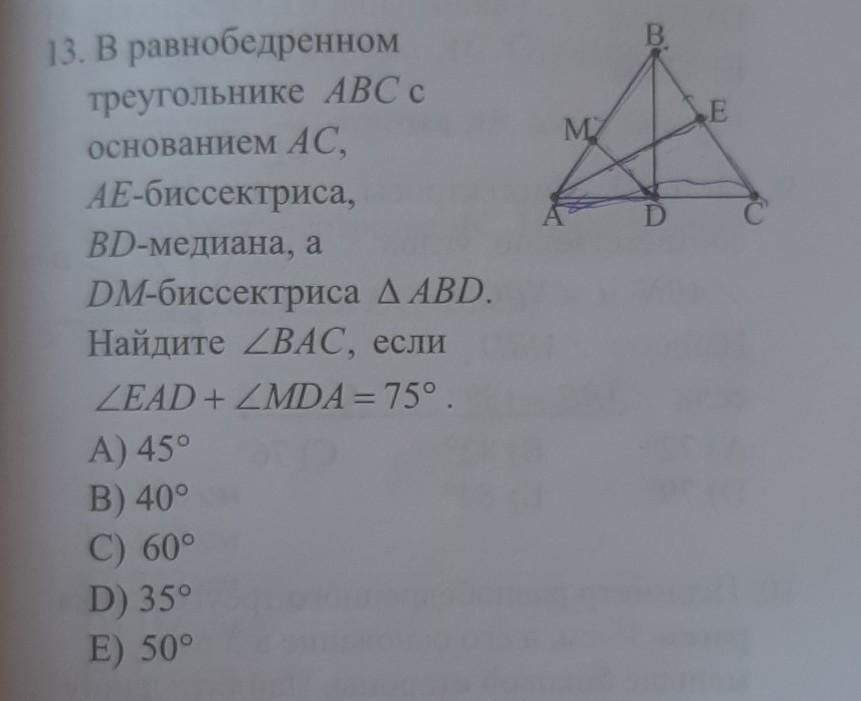
В равнобедренном
треугольнике ABC с
основанием AC,
АЕ-биссектриса,
BD-медиана, а
DM-биссектриса ABD.
Найдите угол BAC, если
угол EAD + уголMDA = 75
Приложения:
NikaZ26:
C) 60
спасибо огромное.
Ответы
Автор ответа:
15
Ответ:
С)60°
С)60°
Объяснение:
BDA=90
DM=биссектриса
MDA=90:2=45
EAD=75-45=30
AE=биссектриса
30*2=60
Я не уверен, но я думаю что ответ 60. Ответ может быть неправильным.
спасибо за ответ и за объяснение.
Автор ответа:
4
Ответ:Треугольник равнобедренный,значит медиана на основание является и перпендикуляром(высотой) на АС,следовательно углы ВDA и BDC равны между собой и равны по 90 градусов
Биссектриса МD поделила угол ВDA на две равные части,угол MDA равен углу МDB и каждый из них равен по 45 градусов
По условию задачи нам известно,что сумма углов ЕАD и MDA равна 75 градусов,угол MDA нам известен,узнаём угол EAD
75-45=30 градусов
По условию известно,что АЕ-биссектриса угла А,значит угол ЕАD-это половина угла А,а сам угол А(ВАС) равен
30•2=60 градусов
Ответ:60 градусов
Объяснение:
Похожие вопросы
Предмет: Математика,
автор: maga198107
Предмет: Геометрия,
автор: virila123
Предмет: Литература,
автор: BelousTatyana70
Предмет: Геометрия,
автор: Erik797
Предмет: География,
автор: marijastrogono