Предмет: Математика,
автор: shahbozm02
Найти обе производные
задание на фото
Приложения:
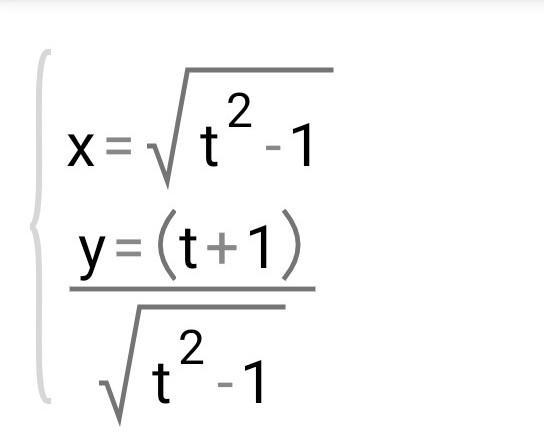
Ответы
Автор ответа:
1
Нужно найти производную параметрически заданной функции.
Формула:
Похожие вопросы
Предмет: Химия,
автор: sashakrokol
Предмет: Математика,
автор: shewchenkomari
Предмет: Русский язык,
автор: Вивена
Предмет: Литература,
автор: Zadumova
Предмет: География,
автор: maria34560