Предмет: Математика,
автор: sakenuke1617
найти решение дифференциальных уравнение
Приложения:
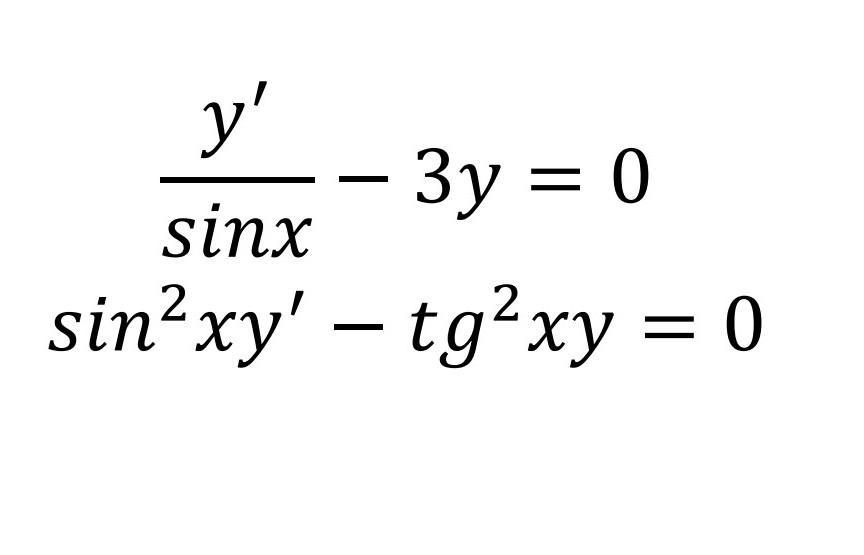
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
оба уравнения - дифференциальные уравнения с разделяющимися переменными
1.
умножаем обе части на sinx и делим на 3у, получим
интегрируем обе части и получаем
⇒
2.
делим на (y*sin²x)
⇒
⇒
⇒
Похожие вопросы
Предмет: Английский язык,
автор: savchinr
Предмет: Химия,
автор: Plug981
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: mkucerenko0ozkftg