Предмет: Математика,
автор: sakenuke1617
найти решение дифференциальных уравнение
Приложения:
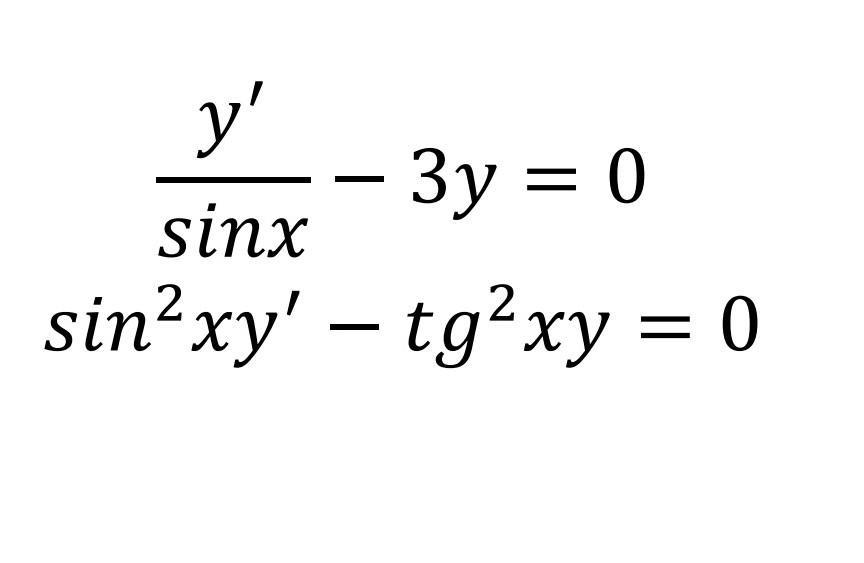
Ответы
Автор ответа:
0
Ответ:
1.
общее решение
2.
общее решение
Похожие вопросы
Предмет: Химия,
автор: Plug981
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: Znanija536
Предмет: Алгебра,
автор: help400