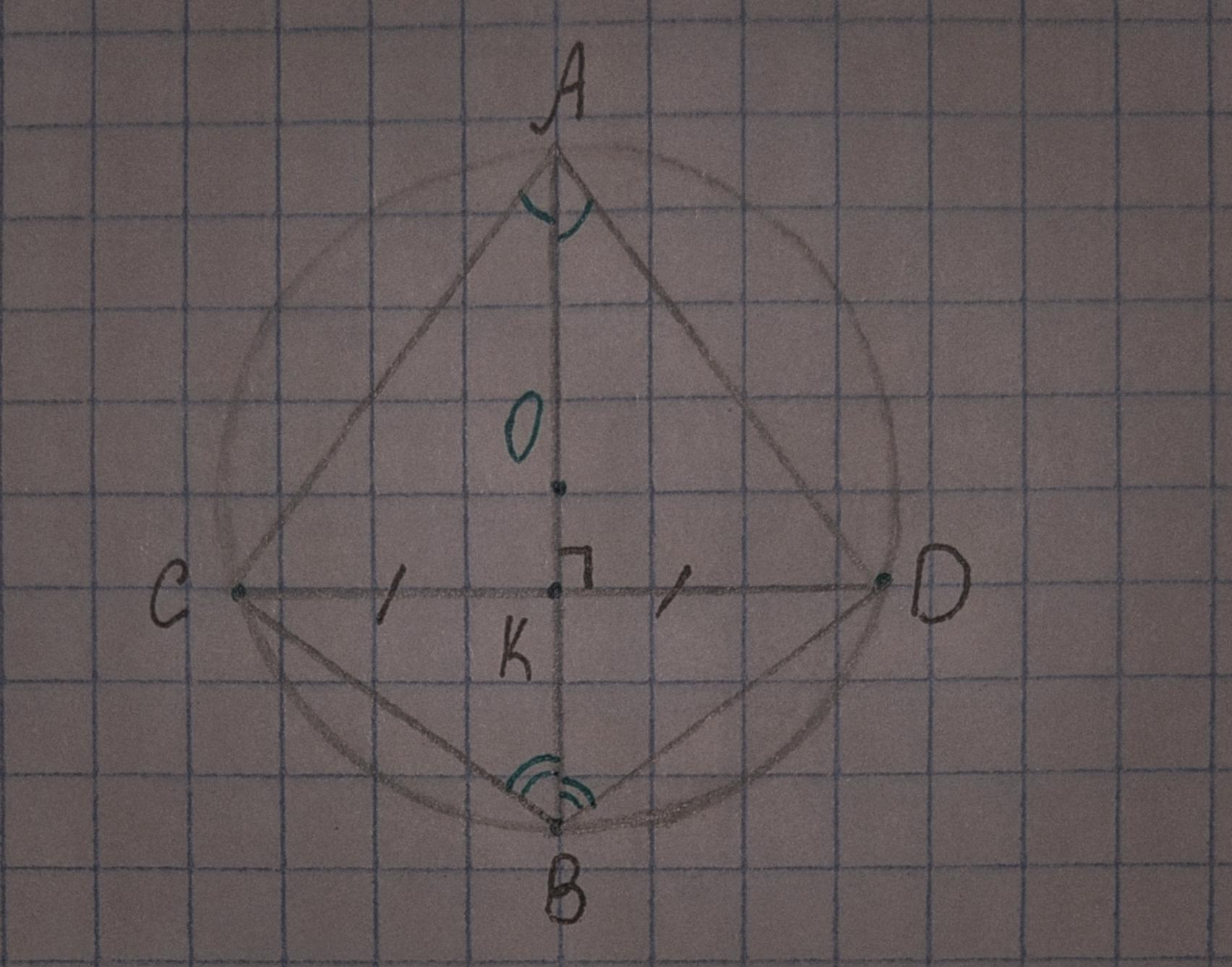Диаметр AB окружности, центром которой является точка O, проходит через середину К хорды CD. Докажите, что треугольник ADB = треугольнику ACB ( очень срочно )
Ответы
1) Теорема: диаметр окружности, проходящий через середину хорды этой окружности, отличной от диаметра, перпендикулярен хорде.
Вследствие этой теоремы при построении чертежа получим ΔАСВ и ΔАDВ, каждый из которых состоит из двух прямоугольных треугольников. ΔАСВ состоит из треугольников ΔАСК и ΔВСК; ΔАDВ состоит из треугольников ΔАDК и ΔВDК.
2) Докажем их равенство попарно.
2.1) Прямоугольные треугольники ΔАСК и ΔАDК имеют общий катет АК и равные по условию катеты КС и КD (т.К - середина СD); значит ΔАСК=ΔАDК по двум катетам.
2.2) Прямоугольные треугольники ΔВСК и ΔВDК имеют общий катет ВК и равные по условию катеты КС и КD (т.К - середина СD); значит ΔВСК=ΔВDК по двум катетам.
3) В равных треугольниках соответственные углы равны. Из равенства первой пары треугольников получаем, что в ΔАСВ и ΔАDВ равны углы ∠САВ и ∠DАВ. Из равенства второй пары треугольников получаем, что в ΔАСВ и ΔАDВ равны углы ∠АВС и ∠АВD.
4) Следствие: ΔАСВ=ΔАDВ по общей стороне АВ и двум прилежащим углам (ч. и т.д.).