Предмет: Математика,
автор: artursakovich04
срочно!!!!!!!!!!!!!!!
Приложения:
Ответы
Автор ответа:
1
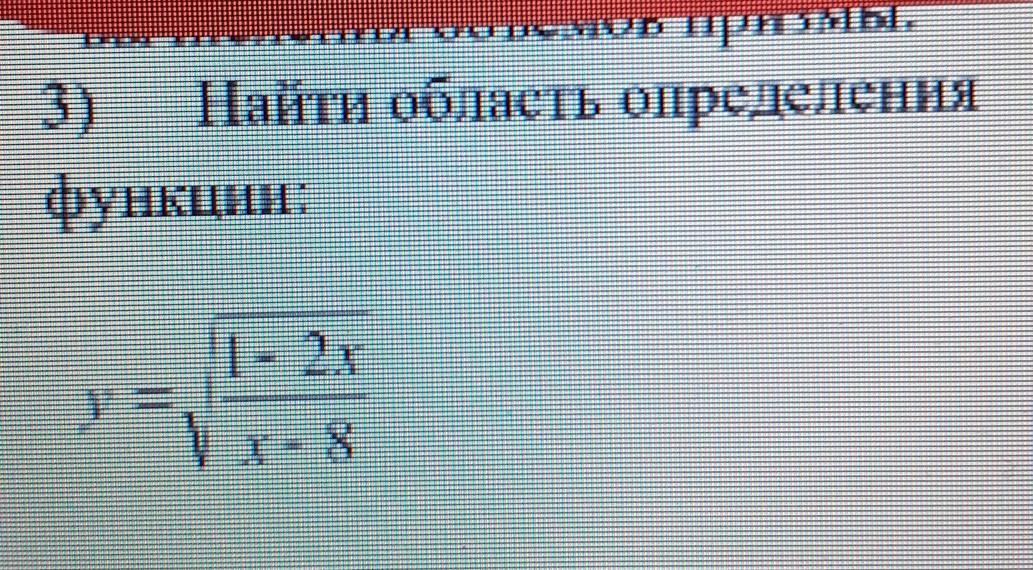
Функция содержит корень квадратный и переменную в знаменателе. Выражение под корнем не может быть отрицательным, и знаменатель не может быть равен нулю.
Найдём нули числителя и знаменателя:
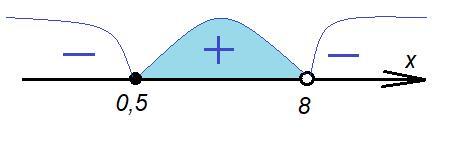
Отметим на числовой оси точки 0,5 (закрашена, так как неравенство не строгое) и 8 (не закрашена, так как превращает знаменатель в ноль). См. приложение.
На каждом из трёх полученных интервалов берём произвольное число и подставляем его в дробь, определяя знак выражения.
Выбираем интервал со знаком плюс.
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: natalevchenya
Предмет: Английский язык,
автор: hsilgne
Предмет: Математика,
автор: pacla
Предмет: Литература,
автор: vladandseva