Предмет: Алгебра,
автор: kusrik
Помогите пожалуйста решить уравнения!
Приложения:
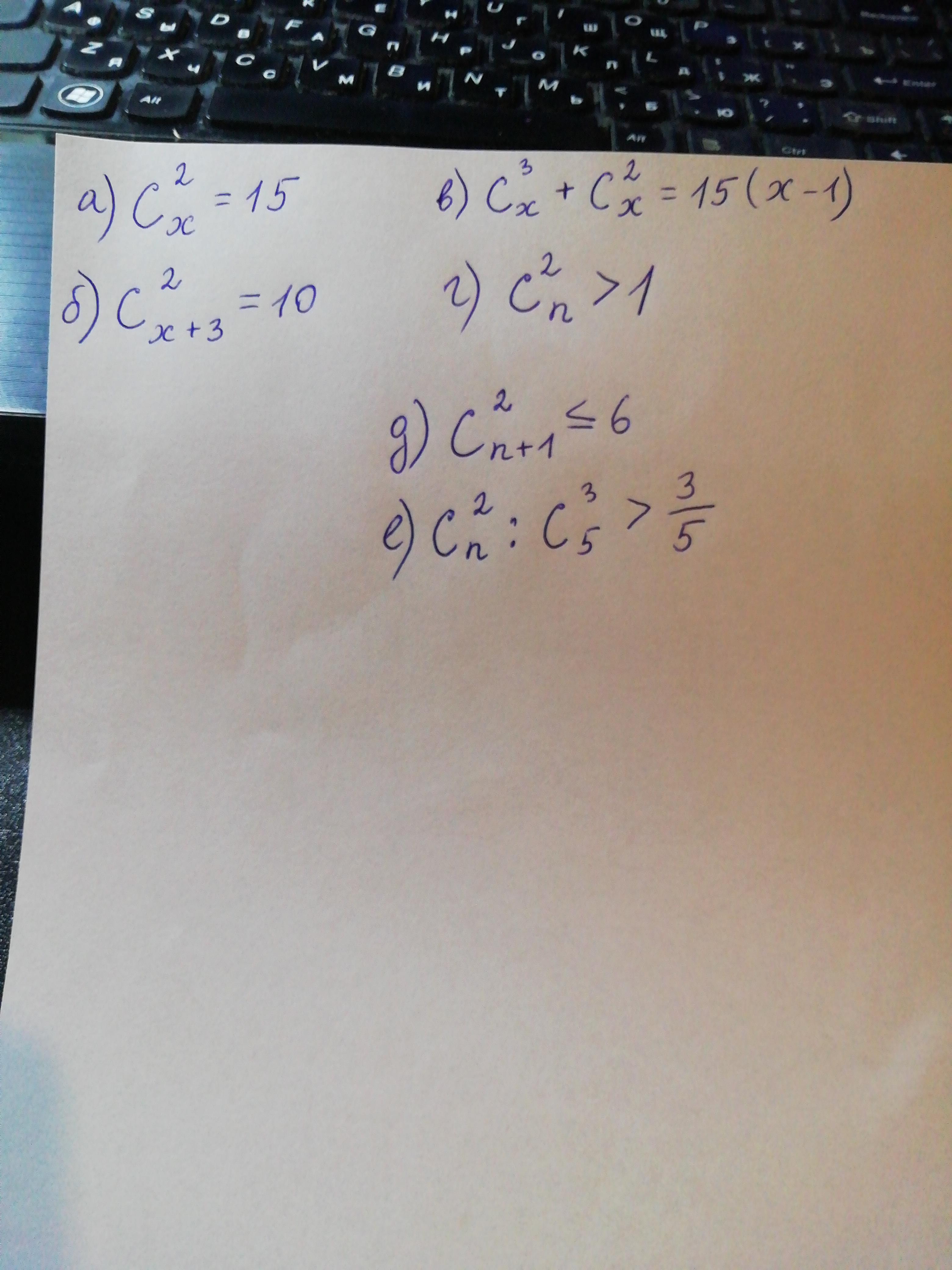
Ответы
Автор ответа:
2
Объяснение:
Ответ: x=6.
Ответ: x=2.
Ответ: x=9.
-∞__+__-1__-__2__+__+∞
n∈(-∞;-1)U(2;+∞) ⇒ n∈(2;+∞).
Ответ: n∈(2;+∞), где n∈N.
-∞__+__-4__-__3__+__+∞
n∈[-4;3] ⇒ n∈[1;3].
Ответ: n=1, 2, 3.
n
-∞__+__-3__-__4__+__+∞
n∈(-∞;-3)U(4;+∞) ⇒ n∈(4;+∞)
Ответ: n∈(4;+∞), где n∈N.
Похожие вопросы
Предмет: Биология,
автор: vfvf5vbz
Предмет: Литература,
автор: Мария984
Предмет: Другие предметы,
автор: 79200880390
Предмет: История,
автор: курбан31
Предмет: Математика,
автор: котейкаTV11