Предмет: Геометрия, автор: Watson134

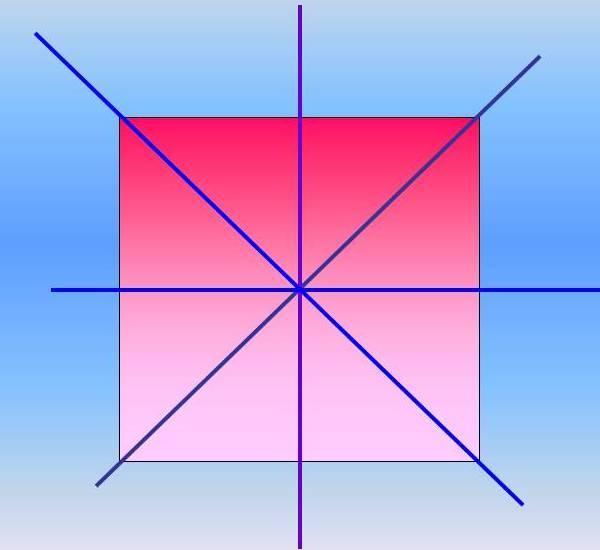
Серединные перепендикуляры к сторонам квадрата пересекаются в точке 0. Докажите,что эта точка принадлежит биссектрисам углов квадрата (нужно очень срочно)

Ответы

Автор ответа: Crzyfizik

1

Ответ:

Точка О, в которой пересекаются серединные перпендикуляры, является центром квадрата, так как оба серединных перпендикуляра являются диаметрами вписанной в квадрат окружности. А диаметры пересекаются в центре окружности, т.е в точке О. Диагонали квадрата, которые являются биссектрисами, будут диаметрами описанной около квадрата окружности, которые тоже будут пересекаться в центре О. Поэтому биссектрисы квадрата и серединные перпендикуляры к сторонам квадрата пересекаются в точке О, Ч.Т.Д.

Объяснение:

Приложения:

Watson134: большое спасибо

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Математика, автор: Savinich

из 90 км пути туристы прошли 72 км. во сколько раз больше весь путь чем непройденная его часть?

2 года назад

Предмет: Биология, автор: Iriska096

Помогите, пожалуйста!!!
Назвіть одноклітинну водорість, яка живе в прісній водоймі.

А фукус

Б ламінарія

В спірогіра

Г хламідомонада

2. Назвіть процес, під час якого рослина вбирає вуглекислий газ і виділяє кисень.

А фотосинтез

Б дихання

В транспірація

Г фототропізм

3. Назвіть речовину, з якої складається зовнішній шар черепашки (мушлі) молюсків.

А рогоподібна

Б вапняк

В перламутр

Г хітин

4. Укажіть тварину, пристосовану до полювання у воді.

А кріт звичайний

Б видра звичайна

В кінь Пржевальського

Г мартишка зелена

5. Назвіть відділ головного мозку, який забезпечує координацію рухів.

А довгастий мозок

Б мозочок

В середній мозок

Г проміжний мозок

6. Укажіть структуру організму людини, у якій утворюються клітини крові.

А червоний кістковий мозок

Б жовтий кістковий мозок

В хрящова тканина

Г окістя

7. Назвіть походження збудника туберкульозу.

А вірус

Б бактерія

В одноклітинна тварина

Г алерген

8. Укажіть елемент будови кістки, який забезпечує її ріст у товщину.

А міжклітинна речовина

Б жовтий кістковий мозок

В хрящова тканина

Г окістя

9. Назвіть кінцевий продукт енергетичного обміну.

А глюкоза

Б гліцерин

В амінокислота

Г вуглекислий газ

10. Назвіть залози, які своїми протоками відкриваються на поверхню шкіри.

А сльозові

Б потові

В ендокринні

Г травні

11. Укажіть фактор, який впливає на частоту дихання.

А якісний склад їжі

Б артеріальний тиск

В інтенсивність реабсорбції

Г вміст СО2 у крові

12. Назвіть залозу, яка виробляє гормон росту.

А гіпофіз

Б епіфіз

В гіпоталамус

Г щитоподібна

Друга частина

13. Назвіть харчові продукти, які виготовляють завдяки життєдіяльності певних бактерій.

А соняшникова олія

Б квашені огірки

В копчена риба

Г пиво

14. Назвіть компонент покритонасінної рослини, не здатний укорінюватися.

А листок

Б квітка

В пагін

Г брунька

15. Назвіть представника типу Членистоногі, органом виділення якого є зелена залоза.

А кліщ собачий

Б жук колорадський

В міль яблунева

Г рак річковий

16. Укажіть особливість будови пінгвінів, яка відрізняє їх від інших видів птахів.

А наявність перетинок між пальцями задніх кінцівок

Б відсутність легеневих мішків

В відсутність бічних борідок у пір’їн

Г здатність пірнати у воду

17. Укажіть камеру серця, у яку надходить венозна кров судинами, що містять внутрішні кишенькові клапани.

А праве передсердя

Б правий шлуночок

В ліве передсердя

Г лівий шлуночок

18. Укажіть орган сечовидільної системи, запалення якого називають «цистит».

А ниркова миска

Б сечовий міхур

В сечовід

Г сечівник

19. Назвіть кістку в складі скелета вільних кінцівок, яка не поєднується суглобами із сусідніми кістками.

А променева

Б надколінок

В мала гомілкова

Г таранна

20. Укажіть елемент будови ока, завдяки якому зображення потрапляє на сітківку в перевернутому вигляді.

А склисте тіло

Б рогівка

В кришталик

Г зіниця

21. Укажіть рису будови, що відрізняє артерії від вен.

А більш товстий шар непосмугованих м’язів

Б наявність у стінках посмугованих м’язів

В відсутність сполучнотканинної оболонки

Г наявність внутрішньої епітеліальної вистилки

22. Назвіть фізіологічний процес, під час якого діафрагма розтягується під тиском органів черевної порожнини.

А глибокий вдих

Б чхання

В спокійний видих

Г спокійний вдих

Третя частина

23. Проаналізуйте твердження щодо об’єктів, зображених на малюнку, і виберіть правильні: І – це плоди квіткових рослин; ІІ – плоди, позначені цифрами 1, 2, 3, – однонасінні; ІІІ – усі плоди соковиті; ІV – плід, позначений цифрою 4, називається «біб».

А тільки І

Б І і ІІ

В І, ІІ, ІІІ

Г І, ІІ, ІV

24. Проаналізуйте твердження стосовно тварини, зображеної на малюнку, і виберіть правильні: І – тварина пристосована до польоту; ІІ – має трикамерне серце; ІІІ – зародок розвивається в яйці; ІV – відсутні зуби.

А І і ІІ

Б І і ІІІ

В І, ІІІ, ІV

Г тільки І

25. Укажіть правильні твердження, які стосуються зображеної на малюнку структури організму людини: І – це будова кісткової тканини; ІІ – це кров людини; ІІІ – цифрою 1 позначено еритроцити; ІV – цифрою 2 позначено остеоцити.

А тільки І

Б тільки ІІ

В ІІ і ІІІ

Г І і ІV

26. Установіть відповідність між кісткою і різновидом з’єднання, яким вона приєднується до сусідньої.

1 лобова А повне зрощення

2 кінцева фаланга пальця Б нерухоме

3 стегнова В напіврухоме

4 грудина Г одноосьовий суглоб

Д багатоосьовий суглоб

27. Розмістіть елементи сенсорної системи рівноваги від першого до останнього згідно з послідовністю сприйняття ними положення тіла в просторі.

А мозок

Б провідні шляхи

В рецепторні клітини

Г отоліти

2 года назад

Предмет: Английский язык, автор: 49r

Как по англизки будет слово"дикобраз"?

2 года назад

Предмет: Литература, автор: unicorn323

25 БАЛЛОВ

Напишите самые значимые по вашему мнению строки из письма Татьяны к Онегину.
(А.С. Пушкин «Евгений Онегин»)

9 лет назад

Предмет: Химия, автор: ganduras2281

Составить 25 уравнений разложения. Разлагаются все основания,карбонаты, сульфиты, силикаты.

9 лет назад