Предмет: Алгебра,
автор: nuriknematov123321
Найти y' и y'"
Найти y' и y"
Приложения:
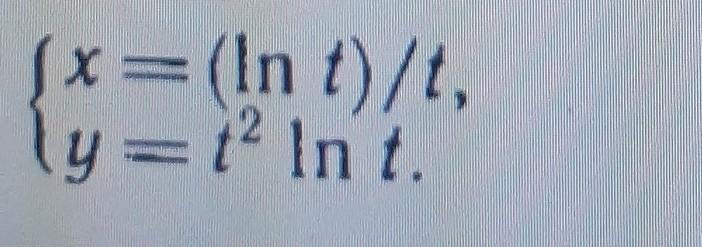
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: alinasaii101
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: annushkamarina
Предмет: Геометрия,
автор: e231ed