Question

помогите, пожалуйста​

Answer 1

Пусть дан треугольник со сторонами $a,b,c\ \ (a=b)$ и периметром P = 28 см. Средняя линия треугольника  m = 4 см.

Найти: $a,b,c.$.

Решение:

Средняя линия треугольника может быть параллельна и равна половине длины любой из трёх сторон.

1) Пусть средняя линия параллельна основанию равнобедренного треугольника  $c$ и равна его половине.

Тогда длина стороны  $c=2m=2\cdot 4=8$ см.

Составим уравнение по условию:

$a+b+8=28\\2a=28-8\\2a=20;\ \ \ \ \boldsymbol{a=b=10}$ см.

Проверим неравенство треугольника (сумма длин меньших двух сторон треугольника должна быть больше длины большей стороны треугольника).

$8+10>10;\ \ \ \ 18>10$  - верно.

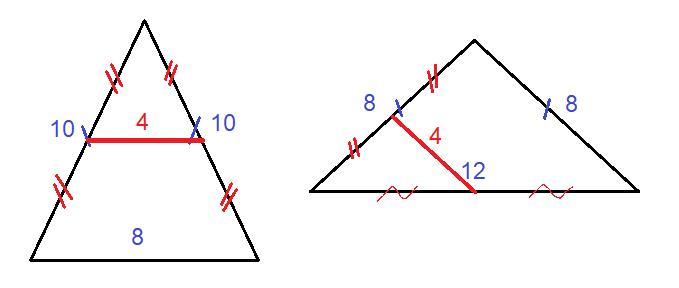
Треугольник со сторонами 8 см, 10 см и 10 см существует. Средняя линия такого равнобедренного треугольника соединяет середины боковых сторон.

2) Пусть средняя линия параллельна любой боковой стороне равнобедренного треугольника $a$ или $b$ и равна их половине.

Тогда длина сторон  $a=b=2m=2\cdot 4=8$ см.

Составим уравнение по условию:

$8+8+c=28\\c=28-8-8;\ \ \ \ \boldsymbol{c=12}$ см.

Проверим неравенство треугольника.

$8+8>12;\ \ \ \ 16>12$  - верно.

Треугольник со сторонами 8 см, 8 см и 12 см существует. Средняя линия такого треугольника соединяет середину боковой стороны и середину основания.

Ответ: 2 решения, 1) 8 см, 10 см, 10 см;  2) 8 см, 8 см, 12 см.