Предмет: Математика,
автор: hbghvgliy
СРОЧНО!!!!!!!!!!Найти пределы, не пользуясь правилом Лопиталя.
Приложения:
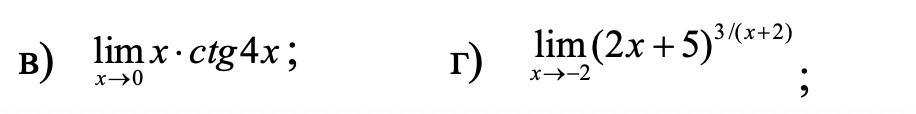
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
в)
sin4x≈ 4x; тогда исходдный предел выглядит так
косинус нуля равен единице, и от него легко избавиться, поскольку у нас х →0), получим
итого
г)
здесь вспоминаем второй замечательный предел
и получаем
и вот
Похожие вопросы
Предмет: Математика,
автор: shark996457
Предмет: Русский язык,
автор: Мифка1
Предмет: Русский язык,
автор: orlovaptica
Предмет: Алгебра,
автор: PERMRUS
Предмет: Химия,
автор: dasew65uyy