Предмет: Алгебра,
автор: 1Panika1
СРОЧНО ПОМОГИТЕ РЕШИТЬ (
Приложения:
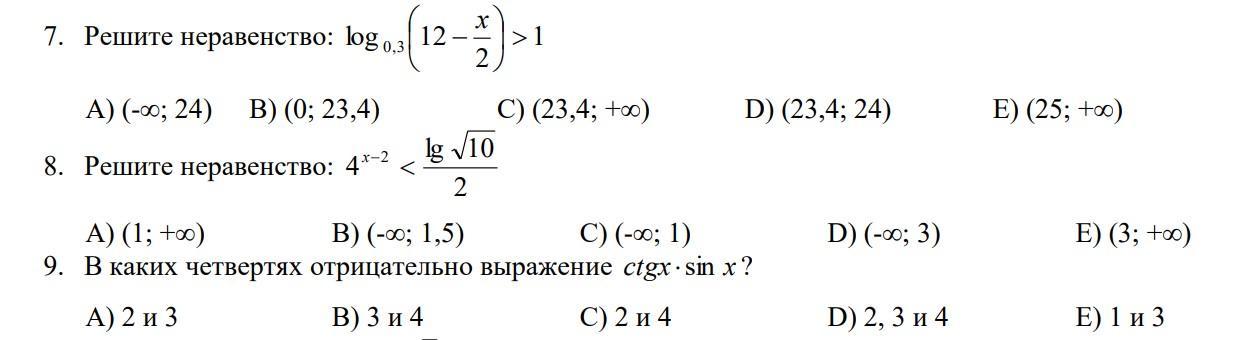
Ответы
Автор ответа:
0
Ответ:7. D; 8. C; 9. A
Объяснение:
Автор ответа:
0
Cosx < 0 во 2 и 3 координатных четвертях.
Похожие вопросы
Предмет: Литература,
автор: Edk1
Предмет: Информатика,
автор: nstrdkn
Предмет: Русский язык,
автор: ира9992
Предмет: Математика,
автор: япростоюля
Предмет: Математика,
автор: Karina12311111