Question

Нужно решить три задания из высшей математики
в 9 задании нужно НАЙТИ ПРОИЗВОДНУЮ

Answer 1

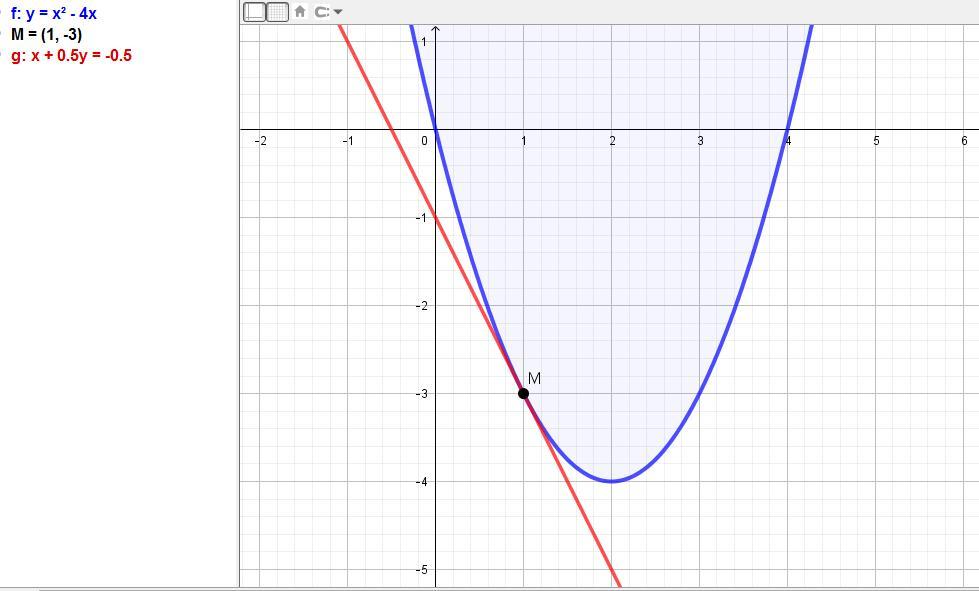
11) Дано уравнение кривой y = x² - 4x и точка М(1; -3).

Производная функции равна:

y' = 2x - 4. в точке х = 1 значение y' = 2*1 - 4 = -2.

Значение функции у = 1² - 4*1 = -3.

Получаем уравнение касательной:

у = -2(х - 1) - 3 = -2х + 2 - 3 = -2х - 1.

Ответ: у = -2х - 1.

Answer 2

Ответ:

9.

$y'_{x} = \frac{y'_{t} }{x'_{t}}$

$x' = \frac{1}{3}(1 - \sqrt{t} ) ^{ \frac{1}{3} - 1 } \times (1 - \sqrt{t})' = \\ = \frac{1}{3} (1 - \sqrt{t} )^ { - \frac{ 2}{3} } \times ( - \frac{1}{2 \sqrt{t} } ) = \\ = \frac{1}{3} \times \frac{1}{ \sqrt[3]{( {1 - \sqrt{t} )}^{2} } } \times ( - \frac{1}{2 \sqrt{t} } ) = \\ = - \frac{1}{6 \sqrt{t} \times \sqrt[3]{( {1 - \sqrt{t} )}^{2} } } = \\ = - \frac{1}{6 \sqrt[6]{ {t}^{3} \times (1 - \sqrt{t} )^{4} } }$

$y' = \frac{1}{2} (1 - \sqrt[3]{t} ) ^{ \frac{1}{2} - 1} \times (1 - \sqrt[3]{t})' = \\ = \frac{1}{2} (1 - \sqrt[3]{t})^{ - \frac{1}{2} } \times ( - \frac{1}{3} \times {t}^{ - \frac{2}{3} } ) = \\ = - \frac{1}{6 \times \sqrt{1 - \sqrt[3]{t}} \times \sqrt[3]{ {t}^{2} } } = \\ = - \frac{1}{6 \times \sqrt[6]{ {t}^{4} \times (1 - \sqrt[3]{t} )^{3}} }$

$y'_{x} = \frac{y'_{t} }{x'_{t}} \\ y'_{x} = \frac{- \frac{1}{6 \times \sqrt[6]{ {t}^{4} \times (1 - \sqrt[3]{t} )^{3}} } }{ - \frac{1}{6 \sqrt[6]{ {t}^{3} \times (1 - \sqrt{t} )^{4} } } } = \\ = \frac{\sqrt[6]{ {t}^{3} \times (1 - \sqrt{t} )^{4} }}{\sqrt[6]{ {t}^{4} \times (1 - \sqrt[3]{t} )^{3}} } = \\ = \frac{ \sqrt[3]{(1 - \sqrt{t}) ^{2} } }{ \sqrt[6]{t \times (1 - \sqrt[3]{t} ) ^{3} } }$

11.

уравнение касательной:

у= f'(x₀)(x - x₀)+f(x₀)

с условия известно : f(x)=x²-4x; x₀=1

f(x₀)=1²-(4×1)=-3

f'(x)=2х-4

f'(x₀)=(2×1)-4=-2

у=-2(х-1)-3=-2х-1

уравнение нормали:

$у= - \frac{1}{f'(x_{0})} (x - x_{0})+f(x_{0})$

$y = \frac{ - 1}{ - 2} (x - 1) - 3 = 0.5 x - 3.5$

13.

у=tg7x

$y'= \frac{7}{ { \cos}^{2} \: 7x }$

$y''= - 7 \frac{{(\cos}^{2} \:( 7x))'}{{{\cos}^{4} \:( 7x) }} = \\ = \frac{ - 7 \times (2 \cos(7x) \times( - 7 \times \sin(7x))) }{{ \cos }^{4}(7x)} = \\ = \frac{98 \sin(7x) }{ { \cos}^{3} (7x)}$